题目内容
在下列关于直线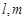 与平面
与平面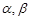 的命题中,正确的是( )
的命题中,正确的是( )
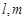 与平面
与平面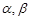 的命题中,正确的是( )
的命题中,正确的是( ) A.若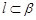 且 且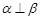 ,则 ,则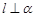 | B.若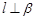 且 且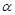 ∥ ∥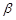 ,则 ,则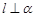 |
C.若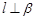 且 且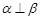 ,则 ,则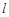 ∥ ∥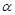 | D.若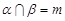 ,且 ,且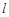 ∥ ∥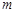 ,则 ,则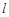 ∥ ∥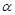 |
B
试题分析:解:A不正确,由面面垂直的性质定理可推出;D不正确,可能
 ;B正确,由线面垂直的定义和定理,面面平行的性质定理可推出;C不正确,由面面垂直的性质定理可知,
;B正确,由线面垂直的定义和定理,面面平行的性质定理可推出;C不正确,由面面垂直的性质定理可知, ,且
,且 ,
, ,则
,则 ;故选B.
;故选B.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目

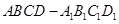 中,
中,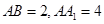 .
. 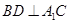 ;
;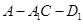 的余弦值;
的余弦值;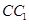 上是否存在点
上是否存在点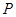 ,使得平面
,使得平面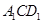
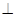 平面
平面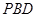 ,若存在,求出
,若存在,求出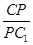 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.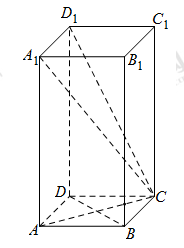
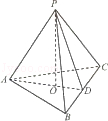
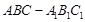 中,
中, 底面
底面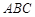 ,
,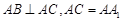 ,E、F分别是棱
,E、F分别是棱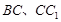 的中点.
的中点.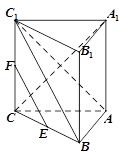
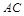 上的点
上的点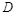 满足平面
满足平面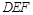 //平面
//平面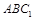 ,试确定点
,试确定点
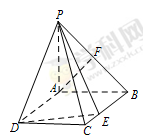
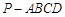 中,底面
中,底面 为矩形,
为矩形,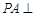 平面
平面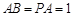 ,
,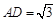 ,
,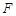 是
是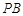 中点,
中点,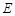 为
为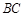 上一点.
上一点.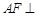 平面
平面 ;
;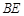 为何值时,二面角
为何值时,二面角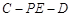 为
为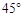 .
.
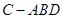 中,
中,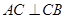 ,
,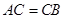 ,
,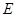 为
为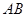 的中点,
的中点,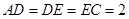 ,
,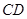 =
=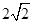 .
.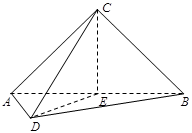
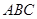 ⊥平面
⊥平面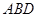 ;
;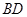 与平面
与平面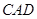 所成角的正弦值.
所成角的正弦值.