化简:$\frac{{2sin+sin2θ}}{{{{cos}^2}\frac{θ}{2}}}$=4sinθ．题目和参考答案——青夏教育精英家教网—

题目内容

12．化简：$\frac{{2sin（{π-θ}）+sin2θ}}{{{{cos}^2}\frac{θ}{2}}}$=4sinθ．

分析直接由三角函数的诱导公式化简计算得答案．

解答解：$\frac{{2sin（{π-θ}）+sin2θ}}{{{{cos}^2}\frac{θ}{2}}}$=$\frac{2sinθ+2sinθcosθ}{\frac{1}{2}（1+cosθ）}=\frac{4sinθ（1+cosθ）}{1+cosθ}$=4sinθ，
故答案为：4sinθ．

点评本题考查了三角函数的诱导公式及化简求值，是基础题．

练习册系列答案

相关题目

2．

在长方体ABCD-A₁B₁C₁D₁中，E，F分别是AB，CD₁的中点，AA₁=AD=1，AB=2．
（1）求证：EF∥平面BCC₁B₁；
（2）求证：平面CD₁E⊥平面D₁DE；
（3）在线段CD₁上是否存在一点Q，使得二面角Q-DE-D₁为45°，若存在，求$\frac{{|{{D_1}Q}|}}{{|{{D_1}C}|}}$的值，不存在，说明理由．

3．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，左焦点为F，过F作垂直于x轴的直线与双曲线相交于B、C两点，若△ABC为直角三角形，则双曲线的离心率为（　　）

20．已知集合A={1，2，3}，B={x|x²-3x+a=0，a∈A}，若A∩B≠∅，则a的值为（　　）

7．在△ABC中，C=$\frac{2π}{3}$，AB=3，则△ABC的周长为（　　）

A．

$6sin（{A+\frac{π}{3}}）+3$

B．

$6sin（{A+\frac{π}{6}}）+3$

C．

$2\sqrt{3}sin（{A+\frac{π}{3}}）+3$

D．

$2\sqrt{3}sin（{A+\frac{π}{6}}）+3$

17．

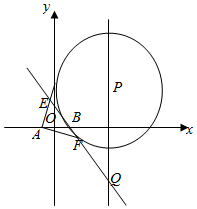如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（-1，0）作圆Γ的两条切线分别与l交于E，F两点．
（1）求证：|EA|+|EB|为定值；
（2）设直线l交直线x=4于点Q，证明：|EB|•|FQ|=|BF•|EQ|．

4．有以下两个推理过程：
（1）在等差数列{a_n}中，若a₁₀=0，则有等式a₁+a₂+…+a_n=a₁+a₂+…+a_19-n（n＜19，n∈N^*）成立．相应地，在等比数列{b_n}中，若b₁₀=1，则有等式b₁b₂…b_n=b₁b₂…b_19-n（n＜19，n∈N^*）；
（2）由1=1²，1+3=2²，1+3+5=3²，1+3+5+…+（2n-1）=n²．
则（1）（2）两个推理过程分别属于（　　）

	A．	归纳推理、演绎推理		B．	类比推理、演绎推理
	C．	归纳推理、类比推理		D．	类比推理、归纳推理

1．

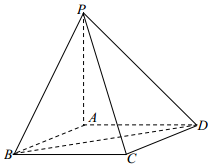在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，PB=PC=PD．
（1）证明：PA⊥平面ABCD；
（2）若PA=2，求二面角A-PD-B的余弦值．

2．设函数f（x）=xlnx，则点（1，0）处的切线方程是x-y-1=0；函数f（x）=xlnx的最小值为-$\frac{1}{e}$．

试题分类