题目内容
7.在△ABC中,C=$\frac{2π}{3}$,AB=3,则△ABC的周长为( )| A. | $6sin({A+\frac{π}{3}})+3$ | B. | $6sin({A+\frac{π}{6}})+3$ | C. | $2\sqrt{3}sin({A+\frac{π}{3}})+3$ | D. | $2\sqrt{3}sin({A+\frac{π}{6}})+3$ |
分析 设△ABC的外接圆半径为R,由已知及正弦定理可求BC=2RsinA=2$\sqrt{3}$sinA,AC=2RsinB=2$\sqrt{3}$sin($\frac{π}{3}$-A),进而利用三角函数恒等变换的应用化简可得周长=2$\sqrt{3}$sin(A+$\frac{π}{3}$)+3,即可得解.
解答 解:设△ABC的外接圆半径为R,则2R=$\frac{3}{sin\frac{2π}{3}}$=2$\sqrt{3}$,
所以:BC=2RsinA=2$\sqrt{3}$sinA,AC=2RsinB=2$\sqrt{3}$sin($\frac{π}{3}$-A),
所以:△ABC的周长=2$\sqrt{3}$(sinA+sin($\frac{π}{3}$-A))+3=2$\sqrt{3}$sin(A+$\frac{π}{3}$)+3.
故选:C.
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
17.若x,y满足条件$\left\{\begin{array}{l}x-y+2≥0\\ x+y-4≤0\\ y≥2\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
2.《九章算术》是我国古代第一部数学专著,全书收集了246个问题及其解法,其中一个问题为“现有一根九节的竹子,自上而下各节的容积成等差数列,上面四节容积之和为3升,下面三节的容积之和为4升,求中间两节的容积各为多少?”该问题中第2节,第3节,第8节竹子的容积之和为( )
| A. | $\frac{17}{6}$升 | B. | $\frac{7}{2}$升 | C. | $\frac{113}{66}$升 | D. | $\frac{109}{33}$升 |
17.若集合A={x||x-1|≤1},B={-2,-1,0,1,2},则集合A∩B=( )
| A. | {0,2} | B. | {-2,2} | C. | {0,1,2} | D. | {-2,-1,0} |
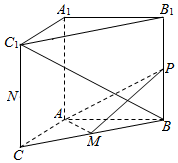 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=$\sqrt{3}$,M为BC的中点,P为侧棱BB1上的动点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1=$\sqrt{3}$,M为BC的中点,P为侧棱BB1上的动点.