题目内容
2.设函数f(x)=xlnx,则点(1,0)处的切线方程是x-y-1=0;函数f(x)=xlnx的最小值为-$\frac{1}{e}$.分析 求出函数的导数,求出切点的导数,得到曲线的斜率,然后求解切线方程;利用导数判断函数的单调性求解函数的最小值即可.
解答 解:求导函数,可得y′=lnx+1
x=1时,y′=1,y=0
∴曲线y=xlnx在点x=1处的切线方程是y=x-1
即x-y-1=0.
令lnx+1=0,可得x=$\frac{1}{e}$,x∈(0,$\frac{1}{e}$),函数是减函数,x>$\frac{1}{e}$时函数是增函数;
所以x=$\frac{1}{e}$时,函数取得最小值:-$\frac{1}{e}$.
故答案为:x-y-1=0;-$\frac{1}{e}$.
点评 本题考查导数知识的运用,考查导数的几何意义,函数的单调性以及最值的求法,求出切线的斜率是关键,

练习册系列答案
相关题目
17.若集合A={x||x-1|≤1},B={-2,-1,0,1,2},则集合A∩B=( )
| A. | {0,2} | B. | {-2,2} | C. | {0,1,2} | D. | {-2,-1,0} |
14.若方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-1}$=1表示焦点在y轴上的椭圆,则k的取值范围是( )
| A. | k<1或k>9 | B. | 1<k<9 | C. | 1<k<9且k≠5 | D. | 5<k<9 |
11.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作,该书中记载有很多数列问题,如“今有女善织,日益功疾.初日织五尺,今一月日织九匹三丈. 问日益几何.”意思是:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加( )(其中1匹=4丈,1丈=10尺,1尺=10寸)
| A. | 5寸另$\frac{15}{29}$寸 | B. | 5寸另$\frac{5}{14}$寸 | C. | 5寸另$\frac{5}{9}$寸 | D. | 5寸另$\frac{1}{3}$寸 |
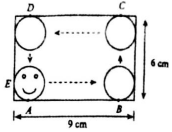 有一个电动玩具,它有一个9×6的长方形(单位:cm)和一个半径为1cm的小圆盘(盘中娃娃脸),他们的连接点为A,E,打开电源,小圆盘沿着长方形内壁,从点A出发不停地滚动(无滑动),如图所示,若此时某人向该长方形盘投掷一枚飞镖,则能射中小圆盘运行区域内的概率为$\frac{40+π}{54}$.
有一个电动玩具,它有一个9×6的长方形(单位:cm)和一个半径为1cm的小圆盘(盘中娃娃脸),他们的连接点为A,E,打开电源,小圆盘沿着长方形内壁,从点A出发不停地滚动(无滑动),如图所示,若此时某人向该长方形盘投掷一枚飞镖,则能射中小圆盘运行区域内的概率为$\frac{40+π}{54}$.