题目内容
3．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点为A，左焦点为F，过F作垂直于x轴的直线与双曲线相交于B、C两点，若△ABC为直角三角形，则双曲线的离心率为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 先求出当x=-c时，y的值，再利用△ABC为直角三角形，建立方程，由此可得双曲线的离心率．
解答 解：由题意，当x=-c时，y=±$\frac{{b}^{2}}{a}$
∵△ABC为直角三角形，
∴$\frac{{b}^{2}}{a}$=a+c
∴c2-a2=a（a+c）
∴c-a=a
∴c=2a
∴e=$\frac{c}{a}$=2
故选：A．
点评 本题考查双曲线的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
13．抛物线y2=8x与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）有相同的焦点，且该焦点到双曲线C的渐近线的距离为1，则双曲线C的方程为（ ）
| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | y2-$\frac{{x}^{2}}{3}$=1 | C． | $\frac{{x}^{2}}{9}$-y2=1 | D． | $\frac{{x}^{2}}{3}$-y2=1 |
14．已知 函数f（x）=sin（x+$\frac{π}{2}$）+cos（x-$\frac{π}{2}$）+m的最大值为2$\sqrt{2}$，则实数m的值为（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | 2 |
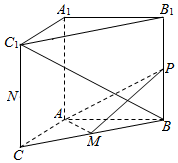如图，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，CAB=90°，AB=AC=2，AA1=$\sqrt{3}$，M为BC的中点，P为侧棱BB1上的动点．
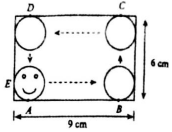有一个电动玩具，它有一个9×6的长方形（单位：cm）和一个半径为1cm的小圆盘（盘中娃娃脸），他们的连接点为A，E，打开电源，小圆盘沿着长方形内壁，从点A出发不停地滚动（无滑动），如图所示，若此时某人向该长方形盘投掷一枚飞镖，则能射中小圆盘运行区域内的概率为$\frac{40+π}{54}$．