题目内容
9.若函数y=f(x)的导数y′=f′(x)仍是x的函数,就把y′=f′(x)的导数y″=f″(x)叫做函数y=f(x)二阶导数,记做y(2)=f(2)(x).同样函数y=f(x)的n-1阶导数的导数叫做y=f(x)的n阶导数,表示y(n)=f(n)(x).在求y=ln(x+1)的n阶导数时,已求得$y'=\frac{1}{x+1},{y^{(2)}}=-\frac{1}{{{{(x+1)}^2}}},{y^{(3)}}=\frac{1•2}{{{{(x+1)}^3}}}$,${y^{(4)}}=-\frac{1•2•3}{{{{(x+1)}^4}}},…$,根据以上推理,函数y=ln(x+1)的第n阶导数为${y^{(n)}}={({-1})^{n-1}}\frac{{({n-1})!}}{{{{({1+x})}^n}}}$.分析 根据导数的计算和归纳推理即可求出答案.
解答 解:求y=ln(x+1)的n阶导数时,已求得$y'=\frac{1}{x+1},{y^{(2)}}=-\frac{1}{{{{(x+1)}^2}}},{y^{(3)}}=\frac{1•2}{{{{(x+1)}^3}}}$,${y^{(4)}}=-\frac{1•2•3}{{{{(x+1)}^4}}},…$,根据以上推理,函数y=ln(x+1)的第n阶导数为 ${y^{(n)}}={({-1})^{n-1}}\frac{{({n-1})!}}{{{{({1+x})}^n}}}$.
故答案为:${y^{(n)}}={({-1})^{n-1}}\frac{{({n-1})!}}{{{{({1+x})}^n}}}$.
点评 本题考查了导数的计算和归纳推理的问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.执行如图所示的程序框图,若输出的S等于$\frac{8}{9}$,则输入的N为( )


| A. | 8 | B. | 9 | C. | 10 | D. | 7 |
20.设x,y满足约束条件$\left\{\begin{array}{l}{y≥0}\\{x-y+1≥0}\\{x+y-3≤0}\end{array}\right.$,则z=2x-y的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 2 |
17.已知集合U=R,函数$y=\sqrt{1-x}$的定义域为M,集合N={x|x2-x≤0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁∪N)=∅ | C. | M∪N=U | D. | M⊆(∁∪N) |
14.已知直线a?平面α,直线b?平面β,α⊥β,则“a⊥b”是“a⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.f(x)=x2+ax+b与坐标轴有三个交点A,B,C,且△ABC外心在y=x上,则a+b=( )
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
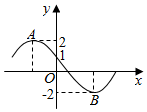 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.