题目内容
10.P是双曲线$\frac{{x}^{2}}{3}$-y2=1的右支上一动点,F是双曲线的右焦点,已知A(3,1)(1)求|PA|+|PF|的最小值;
(2)求|PA|-|PF|的最大值;
(3)求|PA|+$\frac{\sqrt{3}}{2}$|PF|的最小值.
分析 (1)设双曲线左焦点为F1,根据双曲线的定义可知|PA|+|PF|=|PF1|-2a+|PA|,进而可知当P、F1、A三点共线时有最小值,根据双曲线方程可求的F1的坐标,此时|PF1|+|PA|=|AF1|,利用两点间的距离公式求得答案.
(2)当P、F、A三点共线时有最大值;
(3)设P到准线的距离为d,则|PA|+$\frac{\sqrt{3}}{2}$|PF|=|PA|+d,过A作准线的垂线,垂足为B,则A,P,B三点共线时|PA|+$\frac{\sqrt{3}}{2}$|PF|最小.
解答 解:(1)设双曲线左焦点为F1,则|PA|+|PF|=|PF1|-2a+|PA|
当P、F1、A三点共线时有最小值,此时F1(-2,0)、A(3,1)
所以PF1|+|PA|=|AF1|=$\sqrt{26}$,而对于这个双曲线,2a=2$\sqrt{3}$,
所以最小值为$\sqrt{26}$-2$\sqrt{3}$;
(2)当P、F、A三点共线时有最大值,此时F(2,0)、A(3,1)
所以|PA|-|PF|的最大值为|AF|=$\sqrt{2}$;
(3)设P到准线的距离为d,则|PA|+$\frac{\sqrt{3}}{2}$|PF|=|PA|+d,
过A作准线的垂线,垂足为B,则A,P,B三点共线时|PA|+$\frac{\sqrt{3}}{2}$|PF|最小,最小值为3-$\frac{3}{2}$=$\frac{3}{2}$.
点评 本题主要考查了双曲线的应用.解题的过程灵活运用了双曲线的定义和用数形结合的方法解决问题.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.执行下图的程序框图,若输入的a,b,k分别是2,1,3,则输出的M=( )
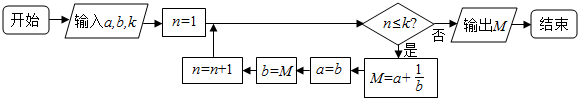
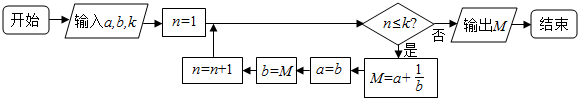
| A. | $\frac{4}{3}$ | B. | $\frac{8}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{15}{8}$ |
7.已知函数f(x)=-x3+6x2-9x+8,则过点(0,0)可以作几条直线与曲线y=f(x)相切( )
| A. | 3条 | B. | 1条 | C. | 0条 | D. | 2条 |
2.已知函数f(x)=asinx-bcosx(a、b为常数,a≠0,x∈R)在x=$\frac{π}{4}$处取得最小值,则函数y=|f($\frac{3π}{4}$-x)|是( )
| A. | 最大值为$\sqrt{2}$b且它的图象关于点(π,0)对称 | |
| B. | 最大值为$\sqrt{2}$a且它的图象关于点($\frac{3π}{4}$,0)对称 | |
| C. | 最大值为$\sqrt{2}$b且它的图象关于直线x=π对称 | |
| D. | 最大值为$\sqrt{2}$a且它的图象关于直线x=$\frac{3π}{4}$对称. |
19.10名运动员中有2名老队员和8名新队员,现从中选3人参加团体比赛,要求老队员至多1人入选且新队员甲不能入选的选法有( )种.
| A. | 77 | B. | 144 | C. | 35 | D. | 72 |