题目内容
15．已知Sn，Tn分别是等差数列{an}，{bn}的前n项和，且$\frac{S_n}{T_n}=\frac{2n+1}{4n-2}（n∈{N^*}）$，则$\frac{a_9}{{{b_1}+{b_{17}}}}+\frac{a_9}{{{b_5}+{b_{13}}}}$=$\frac{35}{66}$．分析 由等差数列的性质可得$\frac{a_9}{{{b_1}+{b_{17}}}}+\frac{a_9}{{{b_5}+{b_{13}}}}$=$\frac{{a}_{9}}{{b}_{9}}$，从而求得．
解答 解：∵数列{an}，{bn}是等差数列，
∴b1+b17=b5+b13=2b9，
∴$\frac{a_9}{{{b_1}+{b_{17}}}}+\frac{a_9}{{{b_5}+{b_{13}}}}$
=$\frac{{a}_{9}}{2{b}_{9}}$+$\frac{{a}_{9}}{2{b}_{9}}$=$\frac{{a}_{9}}{{b}_{9}}$
=$\frac{17{a}_{9}}{17{b}_{9}}$=$\frac{{S}_{17}}{{T}_{17}}$=$\frac{2×17+1}{4×17-2}$=$\frac{35}{66}$，
故答案为：$\frac{35}{66}$．
点评 本题考查了等差数列的性质的应用，属于中档题．
练习册系列答案
走进文言文系列答案
相关题目
6．已知数列{an}中，a1=$\frac{4}{5}$，an+1=$\left\{\begin{array}{l}{2{a}_{n}，0≤{a}_{n}≤\frac{1}{2}}\\{2{a}_{n}-1，\frac{1}{2}＜{a}_{n}≤1}\end{array}\right.$，则a2015=（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
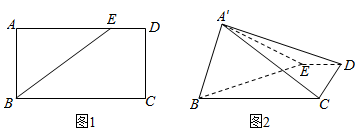
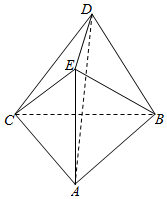如图，在空间几何体ABCDE中，平面ABC⊥平面BCD，AE⊥平面ABC．