题目内容
4.已知f(x)是定义在[-2,2]上的奇函数,当x∈[-2,0)时,f(x)=-ax2-ln(-x)+1,a∈R.(1)当$a=\frac{1}{2}$时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若对于(0,2]上任意的x,都有|f(x)+x|≥1成立,求实数a的最大值.
分析 (1)运用奇函数的定义,可得x∈(0,2]时,f(x)=ax2+lnx-1,求出f(x)的导数,求得切线的斜率和切点,由点斜式方程可得切线的方程;
(2)由题意可得ax2+lnx+x-2≥0或ax2+lnx+x≤0对于任意的x∈(0,2]成立,可得$a≥\frac{-lnx-x+2}{x^2}$或$a≤\frac{-lnx-x}{x^2}$对于任意的x∈(0,2]成立,分别求出表达式右边的最值,由恒成立思想即可得到所求a的范围.
解答 解:(1)f(x)为[-2,2]上的奇函数,则f(-x)=-f(x).
当x∈(0,2]时,-x∈[-2,0),f(x)=-f(-x)=ax2+lnx-1.
当$a=\frac{1}{2}$时,x∈(0,2]时,$f'(x)=x+\frac{1}{x}$,f′(1)=2,$f(1)=-\frac{1}{2}$.
所以,曲线y=f(x)在点(1,f(1))处的切线方程为4x-2y-5=0;
(2)由题可知,|ax2+lnx+x-1|≥1对于任意的x∈(0,2]成立,
即ax2+lnx+x-2≥0或ax2+lnx+x≤0对于任意的x∈(0,2]成立,
可得$a≥\frac{-lnx-x+2}{x^2}$或$a≤\frac{-lnx-x}{x^2}$对于任意的x∈(0,2]成立,
①显然函数$y=\frac{-lnx-x+2}{x^2}$没有最大值,故不存在实数a满足题意;
②设$g(x)=\frac{-lnx-x}{x^2}$,x∈(0,2].$g'(x)=\frac{2lnx+x-1}{x^3}$,x∈(0,2],
令g′(x)=0,得x=1.
当x∈(0,1),g'(x)<0,函数g(x)单调递减;
当x∈(1,2],g'(x)>0,函数g(x)单调递增.
可得a≤g(x)min=g(1)=-1.
综上,实数a的最大值为-1.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用构造函数,由导数判断单调性求得最值,考查化简整理的运算能力,属于中档题.

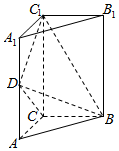 如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.
如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.(1)证明:DC1⊥BC;
(2)求三棱锥C-BDC1的体积.
| A. | 31 | B. | -23 | C. | -5或$\frac{5}{2}$ | D. | 5或-$\frac{5}{2}$ |
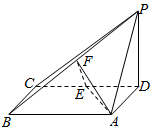 四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点. 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,E是BC的中点,现沿AD将平面PAD折起,使得PA⊥AB;