题目内容
3.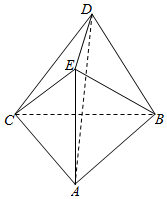 如图,在空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.
如图,在空间几何体ABCDE中,平面ABC⊥平面BCD,AE⊥平面ABC.(1)证明:AE∥平面BCD;
(2)若△ABC为边长为2的正三角形,DE∥平面ABC,AD与BD,CD所成角的余弦值均为$\frac{{\sqrt{2}}}{4}$,求三棱锥D-BEC的体积.
分析 (1)过D作DO⊥BC,则由平面ABC⊥平面BCD得出DO⊥平面ABC,又AE⊥平面ABC,故DO∥AE,于是AE∥平面BCD;
(2)连结OA,则可证四边形OAED是矩形,故DE⊥平面BCD.由AD与BD,CD的夹角相等得OD为∠BDC的角平分线,令DO=a,用a表示出CD,AD,在△ACD中利用余弦定理解出a,代入棱锥的体积公式计算.
解答  (1)证明:过点D作DO⊥BC交BC于点O.
(1)证明:过点D作DO⊥BC交BC于点O.
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,DO?平面BCD,DO⊥BC,
∴DO⊥平面ABC,又∵AE⊥平面ABC,
∴AE∥DO.又DO?平面BCD,AE?平面BCD,
∴AE∥平面BCD.
(2)连接AO,∵DE∥平面ABC,DE?平面OAED,平面OAED∩平面ABC=OA,
∴DE∥OA,又∵AE∥DO,AE⊥平面ABC,
∴四边形AODE是矩形,
∴DE⊥平面BCD.
∵AD与BD,CD所成角的余弦值均为$\frac{{\sqrt{2}}}{4}$,
∴BD=CD,∴O为BC中点,
设DO=a,则OB=OC=$\frac{1}{2}BC=1$,OA=$\sqrt{3}$.cos∠ADC=$\frac{\sqrt{2}}{4}$.
∴$CD=\sqrt{1+{a^2}},AD=\sqrt{3+{a^2}}$.DE=OA=$\sqrt{3}$.
在△ACD中,AC=2,
由余弦定理得:AC2=AD2+CD2-2AD•CD•cos∠ADC,
即4=a2+1+a2+3-2$\sqrt{{a}^{2}+1}$$•\sqrt{{a}^{2}+3}$•$\frac{\sqrt{2}}{4}$,
解得a=1,即DO=1.
∴VD-BEC=VE-BCD=$\frac{1}{3}{S}_{△BCD}•DE$=$\frac{1}{3}×\frac{1}{2}×2×1×\sqrt{3}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行的判定,面面垂直的性质,线面垂直的判定,棱锥的体积计算,属于中档题.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$或$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
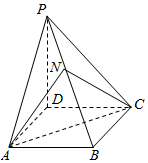 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:6 | D. | 1:8 |
| A. | 31 | B. | -23 | C. | -5或$\frac{5}{2}$ | D. | 5或-$\frac{5}{2}$ |
 如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.
如图,已知四棱锥S-ABCD,底面ABCD是边长为2的棱形,∠ABC=60°,侧面SAD为正三角形,侧面SAD⊥底面ABCD,M为侧棱SB的中点,E为线段AD的中点.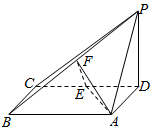 四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.
四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E,F分别为CD,PB的中点.