题目内容
设定义在R上的函数f（x）对任意实数x满足f（x）=f（x-2）+3，且f（2）=4，则f（4）=（ ）
| A、10 | B、7 | C、4 | D、-1 |
考点：抽象函数及其应用
专题：函数的性质及应用
分析：利用f（x）=f（x-2）+3，且f（2）=4，将f（4）逐步转化到f（2）上来，即f（4）=f（4-2）+3=f（2）+3，则f（4）可求．
解答：
解：因为函数f（x）对任意实数x满足f（x）=f（x-2）+3，且f（2）=4
所以f（4）=f（4-2）+3=f（2）+3=4+3=7．
故选：B．
所以f（4）=f（4-2）+3=f（2）+3=4+3=7．
故选：B．
点评：本题考查了抽象函数问题，要仔细体会f（x）=f（x-2）+3在求值中的作用．
练习册系列答案
智慧小复习系列答案
相关题目
若α的终边经过点P（3，-4），则tan（α+
）=（ ）
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
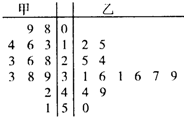某化肥厂甲、乙两个车间包装肥料，在自动包装传送带上每隔30min抽取一包产品，称其重量，用茎叶图分别记录抽查数据如下：