题目内容
2.某科技小组有6名同学,现从中选出3人去参观展览,至少有1名女生入选时的不同选法有16种,则小组中的女生数目为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设出女生的人数为n,由题意知本题要求至少有1位女生的选法有16种,写出所有的选法减去没有女生的选法结果等于16,解方程即可.
解答 解:设女生的人数为n,
由题意知本题要求至少有1位女生的选法有16种,
写出所有的选法减去没有女生的选法结果等于16,有C63-C6-n3=16,
∴C6-n3=4,
∴n=2,
故选:A.
点评 本题考查的是排列问题,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,本题是一个中档题.

练习册系列答案
相关题目
13.△ABC中,∠A=$\frac{π}{6}$,BC=1,AB=$\sqrt{2}$,则∠C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
17.已知tanθ=4,$\frac{1+cos2θ+8si{n}^{2}θ}{sin2θ}$的值是( )
| A. | $\frac{20\sqrt{3}}{3}$ | B. | $\frac{65}{4}$ | C. | 4 | D. | 4$\sqrt{2}$ |
7.若等比数列{an}的前项和为Sn,且$\frac{{s}_{10}}{{s}_{20}}$=$\frac{2}{3}$,则$\frac{{s}_{20}}{{s}_{40}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{4}$ |
11.如图,函数的图象在P点处的切线方程是y=-x+8,若点P的横坐标是5,则f(5)+f′(5)=( )
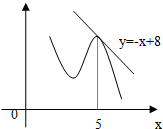

| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 0 |
12.函数f(x)=lg(lgx)的定义域为( )
| A. | (0,+∞) | B. | (0,1) | C. | (0,1] | D. | (1,+∞) |