题目内容
14.已知等差数列{an}满足a3=15,a10=1,且Sn是{an}的前n项和.(1)求{an}的通项公式;
(2)若Sk=-21,求k;
(3)求此数列的前n项和Sn的最大值.
分析 (1)由题意和通项公式可得公差d,可得通项公式;
(2)由(1)可知a1=19,d=-2,可得Sk=19k+$\frac{k(k-1)}{2}$×(-2)=-21,解关于k的方程可得;
(3)解不等式可得等差数列{an}前10项为正数,从第11项开始为负数,可得数列的前10项和最大,由求和公式计算即可.
解答 解:(1)∵等差数列{an}满足a3=15,a10=1,
∴公差d=$\frac{{a}_{10}-{a}_{3}}{10-3}$=-$\frac{15-1}{7}$=-2,
∴an=15-2(n-3)=-2n+21;
(2)由(1)可知a1=19,d=-2,
∴Sk=19k+$\frac{k(k-1)}{2}$×(-2)=-21,
解方程可得k=21,或k=-1(舍去);
∴k=21;
(3)令an=-2n+21≥0,解得n≤$\frac{21}{2}$,
∴递减的等差数列{an}前10项为正数,从第11项开始为负数,
∴数列的前10项和最大,S10=19×10+$\frac{10×9}{2}$×(-2)=100.
点评 本题考查等差数列的通项公式和求和公式,涉及等差数列项的符号,属基础题.

练习册系列答案
相关题目
5.下列各组函数中是同一函数的是( )
| A. | f(x)=x0,g(x)=1 | B. | f(x)=$\sqrt{x+1}$-$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ | ||
| C. | f(x)=$\left\{\begin{array}{l}{1(x<0)}\\{-x(x>0)}\end{array}\right.$,g(t)=$\frac{|t|}{t}$ | D. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ |
9.若α,β为锐角,且满足cosα=$\frac{4}{5}$,cos(α+β)=$\frac{3}{5}$,则sinβ的值为( )
| A. | $\frac{17}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{1}{5}$ |
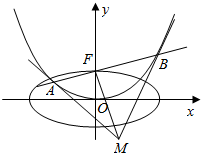 已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.
已知抛物线C:x2=2py(p>0)的焦点为F(0,1),过点F作直线l交抛物线C于A,B两点.椭圆E的中心在原点,焦点在x轴上,点F是它的一个顶点,且其离心率$e=\frac{{\sqrt{3}}}{2}$.