题目内容
12.如图是一个判断是否存在以a,b,6为三边长的钝角三角形的框图(其中a和b是不超过6的正实数).
(1)请你将判断框中的内容补充完整;
(2)如果a和b是通过分别抛掷两个均匀的般子而得到的,求形成钝角三角形的概率;
(3)如果a和b都是[0,6]中均匀分布的随机数且相互独立,求形成钝角三角形的概率.
分析 (1)根据三角形任意两边之和大于第三边,及钝角三角形满足a2+b2<36,可补充完整个框图;
(2)计算所有基本事件个数,及满足a+b>6且a2+b2<36的基本事件个数,代入古典概型概率计算公式,可得答案;
(3)计算所有基本事件对应的面积,及满足a+b>6且a2+b2<36的基本事件对应的面积,代入几何概型概率计算公式,可得答案.
解答 解:(1)将判断框中的内容补充完整后的框图为: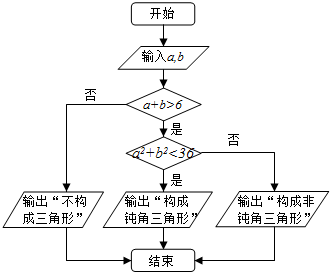
(2)如果a和b是通过分别抛掷两个均匀的般子而得到的,
则共有36种不同的情况,
其中形成钝角三角形,即满足a+b>6且a2+b2<36的有:
(2,5),(3,4),(3,5),(4,3),(4,4),(5,2),(5,3),共7种,
故形成钝角三角形的概率P=$\frac{7}{36}$,
(3)(3)如果a和b都是[0,6]中均匀分布的随机数且相互独立,
则所有情况对应的平面区域的面积S=6×6=36,
其中形成钝角三角形,即满足a+b>6且a2+b2<36的平面区域的面积:
S=$\frac{1}{4}$×π×62-$\frac{1}{2}×6×6$=9π-18,
故形成钝角三角形的概率P=$\frac{9π-18}{36}$=$\frac{π-2}{4}$
点评 本题考查的知识点是概率和算法,熟练掌握古典概型和几何概型的适用范围及解答步骤是解答的关键.

练习册系列答案
相关题目
2.sin70°cos10°+cos110°sin10°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
3.已知集合A={x|ax2-3x+2=0,a∈R},若集合A中至多有一个元素,则实数a的值是( )
| A. | a=0 | B. | a≥$\frac{9}{8}$ | C. | a=0或a≥$\frac{9}{8}$ | D. | 不确定 |
1.圆台的上、下底面面积分别为4和16,中截面把圆台分成两部分,则这两部分的体积之比为( )
| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |