题目内容
1.圆台的上、下底面面积分别为4和16,中截面把圆台分成两部分,则这两部分的体积之比为( )| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |
分析 将棱台还原成棱锥,AA1、BB1、CC1分别是轴截面与小锥、中锥、大锥底面的交线,求出AA1:BB1:CC1=1:$\frac{3}{2}$:2=2:3:4,即可求棱台被它的中截面分成的上、下两部分体积之比.
解答  解:将棱台还原成棱锥,AA1、BB1、CC1分别是轴截面与小锥、中锥、大锥底面的交线,
解:将棱台还原成棱锥,AA1、BB1、CC1分别是轴截面与小锥、中锥、大锥底面的交线,
则AA1:CC1=2:4=1:2.
∵BB1为棱台轴截面的中位线,∴AA1:BB1:CC1=1:$\frac{3}{2}$:2=2:3:4.
∴V小:V中:V大=23:33:43=8:27:64,
∴(V中-V小):(V大-V中)=(27-8):(64-27)=19:37,
即上、下两部分体积之比为19:37.
故选:D.
点评 本题考查求棱台被它的中截面分成的上、下两部分体积之比,考查学生的计算能力,是中档题.

练习册系列答案
相关题目
6.正方体中相邻两个面上的对角线所成的角的大小为( )
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
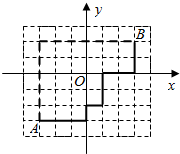 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.