题目内容
对于方程为
+
=1的曲线C给出以下三个命题:
(1)曲线C关于原点中心对称;
(2)曲线C关于x轴对称,也关于y轴对称,且x轴和y轴是曲线C仅有的两条对称轴;
(3)若分别在第一、第二、第三、第四象限的点M,N,P,Q,都在曲线C上,则四边形MNPQ每一条边的边长都大于2;
其中正确的命题是( )
| 1 |
| |x| |
| 1 |
| |y| |
(1)曲线C关于原点中心对称;
(2)曲线C关于x轴对称,也关于y轴对称,且x轴和y轴是曲线C仅有的两条对称轴;
(3)若分别在第一、第二、第三、第四象限的点M,N,P,Q,都在曲线C上,则四边形MNPQ每一条边的边长都大于2;
其中正确的命题是( )
| A、(1)(2) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(2)(3); |
考点:命题的真假判断与应用,曲线与方程
专题:作图题,简易逻辑
分析:分x>0,y>0,x<0,y>0,x<0,y<0,x>0,y<0四类讨论,作出
+
=1的图象,再分别对选项(1)(2)(3)判断即可.
| 1 |
| |x| |
| 1 |
| |y| |
解答:
解:∵
+
=1,
∴当x>0,y>0时,
+
=1⇒
+
=1,解得y=
=1+
;
同理可得,当x<0,y>0时,
+
=1⇒-
+
=1,整理得:y=1-
;
当x<0,y<0时,
+
=1⇒-
-
=1,整理得:y=-1+
;
x>0,y<0时,
+
=1⇒
-
=1,整理得:y=-1-
;
作出图象如下:
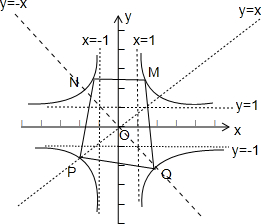
由图可知,曲线C关于原点成中心对称,故(1)正确;
曲线C关于x轴对称,也关于y轴对称,也关于直线y=x与y=-x对称,故(2)错误;
由于在第一、第二、第三、第四象限的点M,N,P,Q,都在曲线C上,由图可知,四边形MNPQ每一条边的边长都大于2,故(3)正确;
综上所述,(1)(3)正确.
故选:B.
| 1 |
| |x| |
| 1 |
| |y| |
∴当x>0,y>0时,
| 1 |
| |x| |
| 1 |
| |y| |
| 1 |
| x |
| 1 |
| y |
| x |
| x-1 |
| 1 |
| x-1 |
同理可得,当x<0,y>0时,
| 1 |
| |x| |
| 1 |
| |y| |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x+1 |
当x<0,y<0时,
| 1 |
| |x| |
| 1 |
| |y| |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x+1 |
x>0,y<0时,
| 1 |
| |x| |
| 1 |
| |y| |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x-1 |
作出图象如下:

由图可知,曲线C关于原点成中心对称,故(1)正确;
曲线C关于x轴对称,也关于y轴对称,也关于直线y=x与y=-x对称,故(2)错误;
由于在第一、第二、第三、第四象限的点M,N,P,Q,都在曲线C上,由图可知,四边形MNPQ每一条边的边长都大于2,故(3)正确;
综上所述,(1)(3)正确.
故选:B.
点评:本题考查命题的真假判断与应用,着重考查曲线与方程的理解与应用,考查分类讨论思想、等价转化思想与数形结合思想的综合运用,属于难题.

练习册系列答案
相关题目
观察下面频率等高条形图,其中两个分类变量C之间关系最强的是( )
A、 |
B、 |
C、 |
D、 |