题目内容
1．已知z=i（1+i），则在复平面内，复数z所对应的点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数的运算法则、几何意义即可得出．
解答 解：z=i（1+i）=-1+i，
则在复平面内，复数z所对应的点（-1，1）在第二象限，
故选：B．
点评 本题考查了复数的运算法则、几何意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
12．执行如图所示的程序框图，若输入A的值为2，则输出P的值为（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
6．执行如图所示的程序框图，其中m=1007${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosxdx，则输出a的结果为（ ）
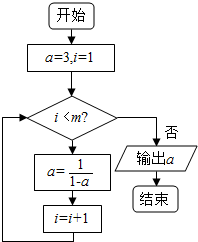
| A． | 3 | B． | -$\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | 2 |
13．2015年9月3号，抗战胜利70周年纪念活动在北京隆重举行，受到全国瞩目，纪念活动包括纪念大会、阅兵式、招待会和文化晚会（招待会和文化晚会算1项活动）等3项，据统计，其中有60名抗战老兵由于身体原因，参加这3项活动的情况如下表所示：
（Ⅰ）若从该60名抗战老兵中按照参加项数分层抽样，抽取6人了解情况．再从抽取的6人中选取2人座谈，求这2人至少1人参加了3项活动的概率；
（Ⅱ）医疗部门决定在（Ⅰ）中抽取到的6名抗战老兵中随机抽取2名进行体检，设参加3项活动的抗战老兵有ξ名接受体检，求ξ的分布列和数学期望．
| 参加纪念活动 项数 | 0 | 1 | 2 | 3 |
| 所占比例 | $\frac{1}{6}$ | $\frac{1}{6}$ | $\frac{1}{3}$ | $\frac{1}{3}$ |
（Ⅱ）医疗部门决定在（Ⅰ）中抽取到的6名抗战老兵中随机抽取2名进行体检，设参加3项活动的抗战老兵有ξ名接受体检，求ξ的分布列和数学期望．