题目内容
6.已知函数f(x)=$\frac{|x|}{x+2}$,若关于x的方程f(x)=kx2有4个不同的实数解,则k的取值范围是( )| A. | k≥1 | B. | k>1 | C. | 0<k<1 | D. | 0<k≤1 |
分析 欲使f(x)=kx2有四个根,即$\frac{|x|}{x+2}$=kx2(*)有四个根,可知x=0是方程(*)的1个根,则只要$\frac{|x|}{x+2}$=kx2有3个根不等于0的根即可.即$\frac{1}{k}=\left\{\begin{array}{l}{x(x+2),x>0}\\{-x(x+2),x<0}\end{array}\right.$,
结合函数g(x)=$\left\{\begin{array}{l}{x(x+2),x>0}\\{-x(x+2),x<0}\end{array}\right.$的图象可求.
解答 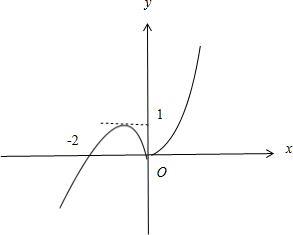 解:f(x)=kx2有四个根,即$\frac{|x|}{x+2}$=kx2(*)
解:f(x)=kx2有四个根,即$\frac{|x|}{x+2}$=kx2(*)
有四个根,
可知x=0是方程(*)的1个根,
则只要$\frac{|x|}{x+2}$=kx2有3个根不等于0的根即可.
即$\frac{1}{k}=\left\{\begin{array}{l}{x(x+2),x>0}\\{-x(x+2),x<0}\end{array}\right.$,
结合函数g(x)=$\left\{\begin{array}{l}{x(x+2),x>0}\\{-x(x+2),x<0}\end{array}\right.$的图象
可得0<$\frac{1}{k}$<1,
∴k>1,
故选:B.
点评 本题主要考查了方程的根与函数交点的相互转化,体现了分类讨论、转化思想与数形结合思想在解题中的应用,属于中档题.

练习册系列答案
相关题目
14.在△ABC中,AB=AC=1,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{BN}$=$\overrightarrow{NC}$,$\overrightarrow{CM}$•$\overrightarrow{AN}$=-$\frac{1}{4}$,则∠ABC=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
18.已知a=2ln3,b=2lg2,c=($\frac{1}{4}$)${\;}^{lo{g}_{\frac{1}{3}}\frac{1}{2}}$,则( )
| A. | c>a>b | B. | a>b>c | C. | a>c>b | D. | b>c>a |
3.设全集U=R,集合A={y|y=x2+1},B={x|x≤-1或x≥3},则A∩(∁UB)=( )
| A. | {x|x≤-1} | B. | {x|x≤1} | C. | {x|-1<x≤1} | D. | {x|1≤x<3} |