题目内容
2.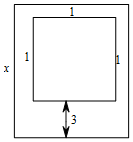 某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,左、右两边及后边与内墙各保留1m宽的通道,前边与内墙保留3m宽的空地(如图所示),其余的地方(图中中间的小矩形)用来种植蔬菜,设矩形温室的一条边长为xm,蔬菜的种植面积为Sm2,当x为何值时,S取得最大值?最大值是多少?
分析 由题意,宽为$\frac{800}{x}$,表示出面积,利用基本不等式,即可得出结论.
解答  解:由题意,宽为$\frac{800}{x}$,
解:由题意,宽为$\frac{800}{x}$,
$S=(x-4)({\frac{800}{x}-2})$$S=800-2x-\frac{3200}{x}+8$,$S=808-2({x+\frac{1600}{x}})$,$S≤808-2×2\sqrt{x•\frac{1600}{x}}=648$,
当且仅当x=40时,符号成立
∴最大为648m2,x=40.
点评 本题考查利用数学知识解决实际问题,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
12. 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
 如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 2,4 | B. | 2,5 | C. | 0,4 | D. | 0,5 |
10. 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )| A. | $\frac{\sqrt{3}}{2}π$ | B. | 4$\sqrt{3}$π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 8$\sqrt{3}$π |
14.在△ABC中,AB=AC=1,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{BN}$=$\overrightarrow{NC}$,$\overrightarrow{CM}$•$\overrightarrow{AN}$=-$\frac{1}{4}$,则∠ABC=( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
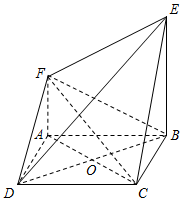 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.