题目内容
已知函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
(1)求a,b的值;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)已知f(t)+f(t-1)<0,求t的取值范围.
| ax+b |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)求a,b的值;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)已知f(t)+f(t-1)<0,求t的取值范围.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:计算题,证明题,函数的性质及应用
分析:(1)由函数f(x)是奇函数可得f(0)=0可求b,由f(
)=
可求a,进而可求f(x);
(2)运用函数的单调性的定义证明:设自变量,作差,变形,定符号,下结论.
(3)由奇函数的定义,得到f(t)<f(1-t),再由函数的单调性,得到不等式组,解出即可.
| 1 |
| 2 |
| 2 |
| 5 |
(2)运用函数的单调性的定义证明:设自变量,作差,变形,定符号,下结论.
(3)由奇函数的定义,得到f(t)<f(1-t),再由函数的单调性,得到不等式组,解出即可.
解答:
(1)解:∵f(x)是定义在(-1,1)上的奇函数,
∴f(0)=0,即有b=0,
又f(
)=
,则
=
,解得a=1.
∴a=1,b=0.
(2)证明:由于f(x)=
,
可设-1<x1<x2<1,
f(x1)-f(x2)=
-
=
,
∵-1<x1<x2<1,
∴x1-x2<0,1-x1x2>0,(x12+1)(x22+1)>0,
∴f(x1)-f(x2)<0,则f(x1)<f(x2),
∴f(x)在(-1,1)上是增函数;
(3)解:∵f(t)+f(t-1)<0,
∴f(t)<-f(t-1)
∵f(x)是定义在(-1,1)上的奇函数,
∴f(t)<f(1-t),
∵f(x)在(-1,1)上是增函数,
∴-1<t<1,且-1<1-t<1,且t<1-t,
∴-1<t<1且0<t<2且t<
,
∴0<t<
.
则t的取值范围是(0,
).
∴f(0)=0,即有b=0,
又f(
| 1 |
| 2 |
| 2 |
| 5 |
| ||
1+
|
| 2 |
| 5 |
∴a=1,b=0.
(2)证明:由于f(x)=
| x |
| 1+x2 |
可设-1<x1<x2<1,
f(x1)-f(x2)=
| x1 |
| 1+x12 |
| x2 |
| 1+x22 |
| (x1-x2)(1-x1x2) |
| (1+x12)(1+x22) |
∵-1<x1<x2<1,
∴x1-x2<0,1-x1x2>0,(x12+1)(x22+1)>0,
∴f(x1)-f(x2)<0,则f(x1)<f(x2),
∴f(x)在(-1,1)上是增函数;
(3)解:∵f(t)+f(t-1)<0,
∴f(t)<-f(t-1)
∵f(x)是定义在(-1,1)上的奇函数,
∴f(t)<f(1-t),
∵f(x)在(-1,1)上是增函数,
∴-1<t<1,且-1<1-t<1,且t<1-t,
∴-1<t<1且0<t<2且t<
| 1 |
| 2 |
∴0<t<
| 1 |
| 2 |
则t的取值范围是(0,
| 1 |
| 2 |
点评:本题主要考查了奇函数的性质:f(0)=0的应用,利用该条件可以简化基本运算,函数单调性的定义的证明及应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,若(a2+c2-b2)sinB=
ac,则角B的值为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
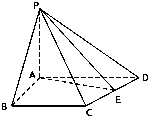 在四棱锥P-ABCD中,侧面PAD与侧面PAB都是以A为直角顶点的直角三角形,底面ABCD是直角梯形,AD∥BC,∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.
在四棱锥P-ABCD中,侧面PAD与侧面PAB都是以A为直角顶点的直角三角形,底面ABCD是直角梯形,AD∥BC,∠ABC=90°,AB=4,BC=3,AD=5,E是CD的中点.