题目内容
14.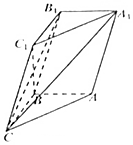 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)若BC=2,∠BCC1=$\frac{π}{3}$,求点B到平面A1B1C的距离.
分析 (Ⅰ)根据本题条件,需要证明BC1⊥AB,由AB⊥侧面BB1C1C就可以解决;而要证明C1B⊥BC,则需要通过解三角形来证明.
(Ⅱ)利用等体积方法,求点B到平面A1B1C的距离.
解答 (Ⅰ)证明:∵CC1=CA,∠BCC1=∠BCA,BC=BC,
∴△ABC≌△C1BC,
∴∠C1BC=∠ABC=90°,∴BC⊥BC1,
∵AB⊥侧面BB1C1C,BC1?面BB1C1C,
∴BC1⊥AB,
∵AB∩BC=B,∴BC1⊥平面ABC;
(Ⅱ)解:若BC=2,∠BCC1=$\frac{π}{3}$,由(Ⅰ)可知CC1=CA=4,AB=2$\sqrt{3}$,
∴${S}_{△{B}_{1}BC}$=$\frac{1}{2}×2×4×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,B1C=$\sqrt{4+16-2×2×4×(-\frac{1}{2})}$=2$\sqrt{7}$,
∴由等体积可得$\frac{1}{3}×2\sqrt{3}×2\sqrt{3}=\frac{1}{3}×\frac{1}{2}×2\sqrt{7}×2\sqrt{3}h$,
∴h=$\frac{2\sqrt{21}}{7}$,即点B到平面A1B1C的距离为$\frac{2\sqrt{21}}{7}$.
点评 本题考查线面垂直、线线垂直,考查锥体体积的计算,考查学生分析解决问题的能力,正确运用线面垂直的判定定理是关键.

练习册系列答案
相关题目
5.设函数f(x)=lg(1+x)-lg(1-x),则函数f(x)是( )
| A. | 偶函数,且在(0,1)上是减函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 奇函数,且在(0,1)上是增函数 |
9.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y-1≥0}\\{y≥\frac{1}{2}x}\\{y≤3}\end{array}\right.$,当目标函数z=ax+by(a>0,b>0)在该约束条件下取得最小值1时,则$\frac{1}{2a}$+$\frac{2}{b}$的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 3+2$\sqrt{2}$ |
19.已知数列{an}满足a1=1,an+1an+Sn=5,则a2=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.复数z满足zi=3+4i,若复数$\overline{z}$对应的点为M,则点M到直线3x-y+1=0的距离为( )
| A. | $\frac{4\sqrt{10}}{5}$ | B. | $\frac{7\sqrt{10}}{5}$ | C. | $\frac{8\sqrt{10}}{5}$ | D. | $\sqrt{10}$ |