题目内容
18.复数z满足zi=3+4i,若复数$\overline{z}$对应的点为M,则点M到直线3x-y+1=0的距离为( )| A. | $\frac{4\sqrt{10}}{5}$ | B. | $\frac{7\sqrt{10}}{5}$ | C. | $\frac{8\sqrt{10}}{5}$ | D. | $\sqrt{10}$ |
分析 利用复数的运算法则、共轭复数的定义、点到直线的距离公式即可得出.
解答 解:由zi=3+4i,得z=$\frac{3+4i}{i}$=$\frac{-i(3+4i)}{-i•i}$=4-3i,
∴$\overline{z}$=4+3i.
∴$\overline{z}$对应的点为M(4,3),
∴所求距离为d=$\frac{|3×4-3+1|}{\sqrt{10}}$=$\sqrt{10}$.
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.在(x-2)6展开式中,二项式系数的最大值为 a,含x5项的系数为b,则$\frac{a}{b}$=( )
| A. | $\frac{5}{3}$ | B. | $-\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
6.设函数f(x)=x•ex,g(x)=x2+2x,$h(x)=2sin(\frac{π}{6}x+\frac{2π}{3})$,若对任意的x∈R,都有h(x)-f(x)≤k[g(x)+2]成立,则实数k的取值范围是( )
| A. | $(-∞,\frac{1}{e}+1]$ | B. | $(-2,\frac{1}{e}+3]$ | C. | $[2+\frac{1}{e},+∞)$ | D. | $[1+\frac{1}{e},+∞)$ |
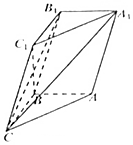 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.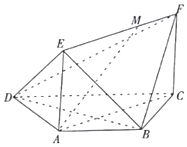 如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.
如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,$∠ADC=\frac{π}{3}$,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=1,点M在线段EF上.