题目内容
5.设函数f(x)=lg(1+x)-lg(1-x),则函数f(x)是( )| A. | 偶函数,且在(0,1)上是减函数 | B. | 奇函数,且在(0,1)上是减函数 | ||
| C. | 偶函数,且在(0,1)上是增函数 | D. | 奇函数,且在(0,1)上是增函数 |
分析 根据题意,首先分析函数的奇偶性,先求出函数的定义域,进而计算可得f(-x)=-f(x),可得函数f(x)为奇函数;再分析函数的单调性,先由对数的运算性质可得f(x)=lg$\frac{1+x}{1-x}$,令t=$\frac{1+x}{1-x}$,则y=lgt,由复合函数的单调性判断方法分析可得函数f(x)在(0,1)上为增函数,综合即可得答案.
解答 解:根据题意,函数f(x)=lg(1+x)-lg(1-x),
有$\left\{\begin{array}{l}{1+x>0}\\{1-x>0}\end{array}\right.$,解可得-1<x<1,
即函数f(x)的定义域为(-1,1),关于原点对称,
f(-x)=lg[1+(-x)]-lg[1-(-x)]=lg(1-x)-lg(1+x)=-f(x),
故函数f(x)为奇函数,
而f(x)=lg(1+x)-lg(1-x)=lg$\frac{1+x}{1-x}$,
令t=$\frac{1+x}{1-x}$,则y=lgt,
当x∈(0,1)时,t=$\frac{1+x}{1-x}$=-$\frac{2}{x-1}$-1,为增函数;
而y=lgt为增函数,
故函数f(x)在(0,1)上为增函数;
故选:D.
点评 本题考查函数奇偶性与单调性的判断,分析奇偶性时需要先分析函数的定义域.

练习册系列答案
相关题目
16.已知复数$\overline{z}$=$\frac{2}{i(3-i)}$,则复数z在复平面内的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.某商场拟对商品进行促销,现有两种方案供选择.每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,顶计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4.第二个月销量是笫一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令ξi(i=1,2)表示实施方案i的第二个月的销量是促销前销量的倍数.
(Ⅰ)求ξ1,ξ2的分布列:
(Ⅱ)不管实施哪种方案,ξi与第二个月的利润之间的关系如表,试比较哪种方案第二个月的利润更大.
(Ⅰ)求ξ1,ξ2的分布列:
(Ⅱ)不管实施哪种方案,ξi与第二个月的利润之间的关系如表,试比较哪种方案第二个月的利润更大.
| 销量倍数 | ξi≤1.7 | 1.7<ξi<2.3 | ξi2.3 |
| 利润(万元) | 15 | 20 | 25 |
17.若复数$\overline{z}$满足|z+i|+|z-i|=2,则复数$\overline{z}$在平面上对应的图形是( )
| A. | 椭圆 | B. | 双曲线 | C. | 直线 | D. | 线段 |
9.在(x-2)6展开式中,二项式系数的最大值为 a,含x5项的系数为b,则$\frac{a}{b}$=( )
| A. | $\frac{5}{3}$ | B. | $-\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $-\frac{3}{5}$ |
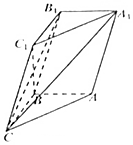 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.