题目内容
4.已知函数f(x)=|x-3|(1)解不等式:f(x)+f(x+1)≤2;
(2)若a<0,求证:f(ax)-f(3a)≥af(x).
分析 (1)分类讨论,解不等式;
(2)由题意得f(ax)-af(x)=|ax-3|-a|x-3|=|ax-3|+|3a-ax|≥|ax-3+3a-ax|=|3a-3|=f(3a),即可证明结论.
解答 (1)解:由题意,得f(x)+f(x+1)=|x-3|+|x-2|,因此只须解不等式|x-3|+|x-2|≤2
当x≤2时,原不等式等价于-2x+5≤2,即$\frac{3}{2}≤x≤2$,
当2<x≤3时,原不等式等价于1≤2,即2<x≤3;
当x>3时,原不等式等价于2x-5≤2,即$3<x≤\frac{7}{2}$.
综上,原不等式的解集为$\left\{{x\left|{\frac{3}{2}≤x≤\frac{7}{2}}\right.}\right\}$.
(2)证明:由题意得f(ax)-af(x)=|ax-3|-a|x-3|=|ax-3|+|3a-ax|≥|ax-3+3a-ax|=|3a-3|=f(3a)
所以f(ax)-f(3a)≥af(x)成立.
点评 本题考查不等式的解法,考查绝对值不等式的性质的运用,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
12.已知函数:①y=x3+3x2;②$y=\frac{{{e^x}+{e^{-x}}}}{2}$;③$y={log_2}\frac{3-x}{3+x}$;④y=xsinx,从中任取两个函数,则这两函数奇偶性相同的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
19.已知变量x,y满足$\left\{\begin{array}{l}x-y≥-2\\ x+y≥-2\\ x≤0\end{array}\right.$则$\frac{y+2}{x+3}$的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 1 |
9.过点P(1,2)的直线与圆x2+y2=1相切,且与直线ax+y-1=0垂直,则实数a的值为( )
| A. | 0 | B. | $-\frac{4}{3}$ | C. | 0或$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
16.已知复数$\overline{z}$=$\frac{2}{i(3-i)}$,则复数z在复平面内的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
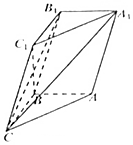 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,CC1=CA,∠BCC1=∠BCA.