题目内容
在 中,三个内角
中,三个内角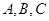 所对边的长分别为
所对边的长分别为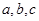 ,已知
,已知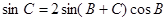 .
.
(Ⅰ)判断 的形状;
的形状;
(Ⅱ)设向量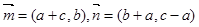 ,若
,若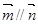 ,求
,求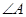 .
.
(1)  为等腰三角形;(2)
为等腰三角形;(2)  .
.
解析试题分析:(1)在三角恒等变换中,往往将左右两边变为齐次式.在本题中,若将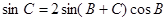 右边展开,则左边为一次式,右边为三次式,这不是我们想要的.
右边展开,则左边为一次式,右边为三次式,这不是我们想要的.
在 中 ,
中 , ,所以
,所以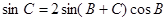 可变为:
可变为: ,这样再展开,左右两边的次便相同,从而可使问题得以解决.
,这样再展开,左右两边的次便相同,从而可使问题得以解决.
(2)由 可得
可得 ,这种等式都用余弦定理.由余弦定理得:
,这种等式都用余弦定理.由余弦定理得: .由此可求出角C.又由(1)得ΔABC是等腰三角形,所以可求出角A.
.由此可求出角C.又由(1)得ΔABC是等腰三角形,所以可求出角A.
试题解析:(1)在 中 ,
中 , ,
, ,
, 为等腰三角形.
为等腰三角形.
(2)由 ,得
,得 .
. ,又
,又 为等腰三角形,
为等腰三角形,  .
.
考点:1、三角函数的计算;2、余弦定理;3、向量的运算.

练习册系列答案
相关题目
 ,求∠C的度数.
,求∠C的度数.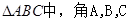 所对的边分别为
所对的边分别为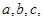 且
且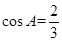 .
. ;
;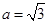 ,求
,求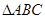 面积的最大值.
面积的最大值.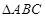 中,角
中,角 、
、 、
、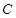 的对边分别为
的对边分别为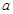 、
、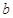 、
、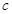 ,且
,且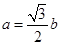 ,
,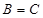 .
.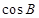 的值;
的值;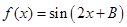 ,求
,求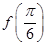 的值.
的值. 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为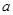 、
、 、
、 ,若
,若 .
. ,求
,求 ,
,
 ,求函数
,求函数 的最大值和最小值,并写出相应的x的值;
的最大值和最小值,并写出相应的x的值; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
, 且
且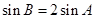 ,求
,求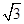 acos C.
acos C.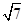 ,且
,且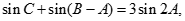 求△ABC的面积.
求△ABC的面积.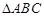 中,角
中,角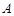 、
、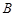 、
、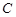 对的边分别为
对的边分别为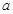 、
、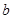 、
、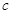 ,且
,且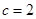 ,
,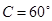 .
.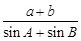 的值;
的值;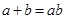 ,求
,求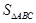 .
. 中,角
中,角 ,
, ,
, 对应的边分别是
对应的边分别是 ,
, ,
, .已知
.已知 .
. ,
, ,求
,求 的值.
的值.