题目内容
在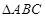 中,角
中,角 、
、 、
、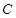 的对边分别为
的对边分别为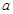 、
、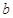 、
、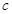 ,且
,且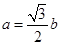 ,
,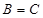 .
.
(Ⅰ)求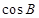 的值;
的值;
(Ⅱ)设函数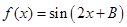 ,求
,求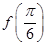 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由已知得 ,又
,又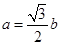 ,所以三角形三边关系确定,利用余弦定理求
,所以三角形三边关系确定,利用余弦定理求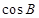 ,(Ⅱ)由(1)可求
,(Ⅱ)由(1)可求 ,又
,又  ,利用和角的正弦公式展开代入即可求
,利用和角的正弦公式展开代入即可求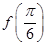 的值.
的值.
试题解析:(Ⅰ) 因为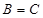 ,所以
,所以 ,又
,又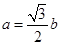 ,所以
,所以 ,
,
(Ⅱ)由(Ⅰ)得 ,所以
,所以


 .
.
考点:1、余弦定理;2、和角的正弦公式;3、同角三角函数基本关系式.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

 中,角
中,角 所对的边分别为
所对的边分别为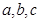 ,且,
,且, .
. 的值;
的值; ,
,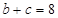 ,求三角形ABC的面积.
,求三角形ABC的面积.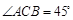 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.
 中,角
中,角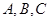 的对边分别为
的对边分别为 ,且满足
,且满足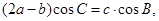
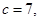
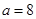 .
.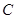 ;
; ,
, ,函数
,函数 .
.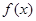 的最大值,并求取最大值时
的最大值,并求取最大值时 的取值集合;
的取值集合; 分别为
分别为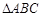 内角
内角 的对边,且
的对边,且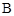 为锐角,且
为锐角,且 ,求
,求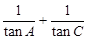 的值.
的值. 中,三个内角
中,三个内角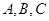 所对边的长分别为
所对边的长分别为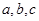 ,已知
,已知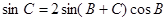 .
.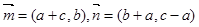 ,若
,若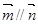 ,求
,求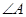 .
.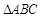 中,已知
中,已知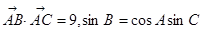 ,又
,又 的面积等于6.
的面积等于6.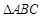 的三边之长;
的三边之长;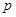 是
是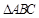 (含边界)内一点,
(含边界)内一点,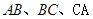 的距离分别为
的距离分别为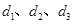 ,求
,求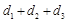 的取值范围.
的取值范围. 中,
中,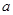 、
、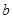 、
、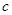 是三个内角
是三个内角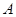 、
、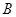 、
、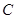 的对边,关于
的对边,关于 的不等式
的不等式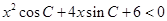 的解集是空集.
的解集是空集.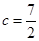 ,
,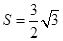 ,求当角
,求当角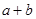 的值.
的值.