题目内容
在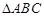 中,角
中,角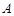 、
、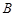 、
、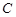 对的边分别为
对的边分别为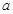 、
、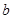 、
、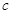 ,且
,且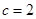 ,
,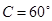 .
.
(1)求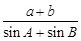 的值;
的值;
(2)若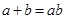 ,求
,求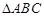 的面积
的面积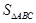 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由正弦定理计算比值 ,确定
,确定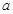 与
与 、以及
、以及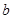 与
与 的等量关系,然后将相应结果代入计算
的等量关系,然后将相应结果代入计算 的值;(2)利用余弦定理
的值;(2)利用余弦定理
 ,再结合已知条件
,再结合已知条件 求出
求出 的值,最后利用三角形的面积公式
的值,最后利用三角形的面积公式
 计算
计算 的面积.
的面积.
试题解析:(1)由正弦定理可得: ,
,
所以 ,
, ,
,
所以 ;
;
(2)由余弦定理得 ,即
,即 ,
,
又 ,所以
,所以 ,解得
,解得 或
或 (舍去),
(舍去),
所以 .
.
考点:1.正弦定理;2.余弦定理;3.三角形的面积

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为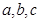 ,且,
,且, .
. 的值;
的值; ,
,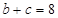 ,求三角形ABC的面积.
,求三角形ABC的面积. 中,三个内角
中,三个内角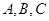 所对边的长分别为
所对边的长分别为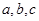 ,已知
,已知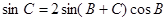 .
.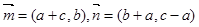 ,若
,若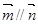 ,求
,求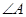 .
.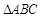 中,已知
中,已知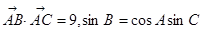 ,又
,又 的面积等于6.
的面积等于6.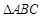 的三边之长;
的三边之长;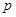 是
是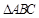 (含边界)内一点,
(含边界)内一点,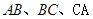 的距离分别为
的距离分别为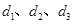 ,求
,求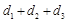 的取值范围.
的取值范围.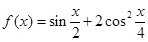
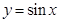 的图像变换得到
的图像变换得到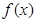 的图像;
的图像;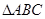 中,角
中,角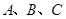 所对的边分别是
所对的边分别是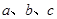 ,若
,若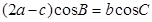 ,求
,求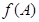 的取值范围
的取值范围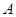 、
、 、
、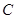 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点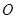 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为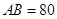
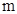 ,
,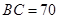
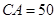
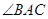 的大小;
的大小;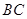 的距
的距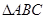 中,设内角
中,设内角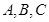 的对边分别为
的对边分别为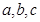 ,向量
,向量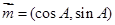 ,向量
,向量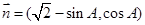 ,若
,若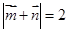
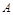 的大小;
的大小;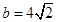 ,且
,且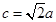 ,求
,求 中,
中,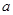 、
、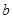 、
、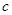 是三个内角
是三个内角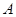 、
、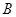 、
、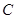 的对边,关于
的对边,关于 的不等式
的不等式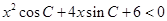 的解集是空集.
的解集是空集.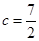 ,
,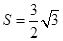 ,求当角
,求当角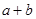 的值.
的值. 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
, ,
, ,
, .
.