题目内容
在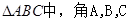 所对的边分别为
所对的边分别为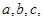 且
且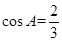 .
.
(1)求 ;
;
(2)若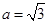 ,求
,求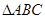 面积的最大值.
面积的最大值.
(1) ;(2)
;(2) 面积的最大值为
面积的最大值为 .
.
解析试题分析:(1)求 ,首先利用三角形内角和等于
,首先利用三角形内角和等于 对其转化成单角,再利用倍角公式进行恒等变化得
对其转化成单角,再利用倍角公式进行恒等变化得 ,由已知
,由已知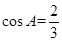 ,带入即可;(2)若
,带入即可;(2)若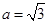 ,求
,求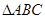 面积的最大值,由已知
面积的最大值,由已知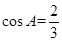 ,可求出
,可求出 ,可利用
,可利用 ,因此求
,因此求 即可,又因为
即可,又因为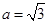 ,可想到利用余弦定理来解,由余弦定理得,
,可想到利用余弦定理来解,由余弦定理得, ,利用基本不等式可求出
,利用基本不等式可求出 的最大值,从而得
的最大值,从而得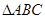 面积的最大值.
面积的最大值.
试题解析:(1)
 6分
6分
(2)
即 ,
, ,
,
 面积的最大值为
面积的最大值为 12分
12分
考点:三角恒等变换,解三角形

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按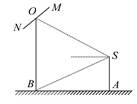
 中,角
中,角 所对的边分别为
所对的边分别为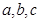 ,且,
,且, .
. 的值;
的值; ,
,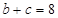 ,求三角形ABC的面积.
,求三角形ABC的面积.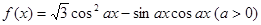 的图像与直线
的图像与直线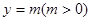 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为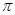 的等差数列.
的等差数列.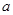 和
和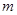 的值;
的值;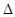 ABC中a、b、c分别是∠A、∠B、∠C的对边.若
ABC中a、b、c分别是∠A、∠B、∠C的对边.若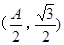 是函数
是函数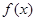 图象的一个对称中心,且a=4,求
图象的一个对称中心,且a=4,求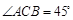 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.
 中,角
中,角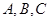 的对边分别为
的对边分别为 ,且满足
,且满足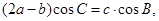
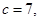
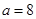 .
.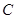 ;
; 中,三个内角
中,三个内角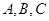 所对边的长分别为
所对边的长分别为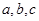 ,已知
,已知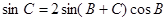 .
.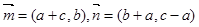 ,若
,若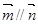 ,求
,求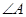 .
.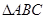 中,设内角
中,设内角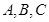 的对边分别为
的对边分别为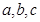 ,向量
,向量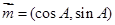 ,向量
,向量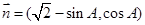 ,若
,若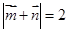
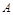 的大小;
的大小;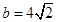 ,且
,且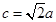 ,求
,求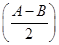 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=-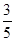 .
. ,b=5,求向量
,b=5,求向量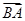 在
在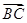 方向上的投影.
方向上的投影.