题目内容
极坐标方程分别为ρ=cosθ与ρ=sinθ的两个圆的圆心距为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把已知给出的极坐标方程两边同时乘以ρ,得到圆的一般式方程,化为标准式求出圆心坐标,由两点间的距离公式得答案.
解答:
解:由ρ=cosθ,得ρ2=ρcosθ,即x2+y2=x,化为圆的标准方程:(x-
)2+y2=
.
圆心坐标为(
,0).
由ρ=sinθ,得ρ2=ρsinθ,即x2+y2=y,化为圆的标准方程:x2+(y-
)2=
.
圆心坐标为(0,
).
∴两个圆的圆心距为
=
.
故答案为:
.
| 1 |
| 2 |
| 1 |
| 4 |
圆心坐标为(
| 1 |
| 2 |
由ρ=sinθ,得ρ2=ρsinθ,即x2+y2=y,化为圆的标准方程:x2+(y-
| 1 |
| 2 |
| 1 |
| 4 |
圆心坐标为(0,
| 1 |
| 2 |
∴两个圆的圆心距为
(
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了简单曲线的极坐标方程,考查了极坐标与直角坐标的互化,是基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
定义
=m1m4-m2m3,将函数f(x)=
的图象向左平移ϕ(ϕ>0)个单位长度后,得到函数g(x),若g(x)为奇函数,则ϕ的值可以是( )
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=
sin2x+cos2x-1的图象向右平移
个单位,所得函数图象的一个对称中心是( )
| 3 |
| π |
| 6 |
| A、(0,-1) | ||
B、(
| ||
C、(
| ||
D、(-
|
图中的小网格由等大的小正方形拼成,则向量
-
=( )

| a |
| b |

| A、e1+3e2 |
| B、-e1-3e2 |
| C、e1-3e2 |
| D、-e1+3e2 |
某几何体的正视图与侧视频如图所示,则该几何体的俯视图不可能是( )

A、 |
B、 |
C、 |
D、 |
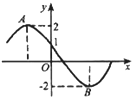 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,| π |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
若函数y=x•2x 且y′=0,则x=( )
A、-
| ||
B、
| ||
| C、-ln2 | ||
| D、ln2 |