题目内容
12.在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点D在BC边上且$\overrightarrow{AD}$=λ($\frac{c}{|c|sinB}+\frac{b}{|b|sinC}$)(λ∈R),则( )| A. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\overrightarrow{b}$ | B. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\overrightarrow{b}$ |
分析 可根据正弦定理得到$\frac{1}{|\overrightarrow{c}|sinB}=\frac{1}{|\overrightarrow{b}|sinC}$,从而便可得出$\overrightarrow{AD}=\frac{λ}{|\overrightarrow{c}|sinB}(\overrightarrow{c}+\overrightarrow{b})$,这样根据点D在边BC上及向量加法的平行四边形法则即可得出$\frac{λ}{|\overrightarrow{c}|sinB}=\frac{1}{2}$,这样即可找出正确答案.
解答 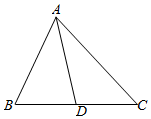 解:如图,
解:如图,
在△ABC中,根据正弦定理得:$\frac{|\overrightarrow{b}|}{sinB}=\frac{|\overrightarrow{c}|}{sinC}$;
∴$\frac{1}{|\overrightarrow{c}|sinB}=\frac{1}{|\overrightarrow{b}|sinC}$;
∴$\overrightarrow{AD}=\frac{λ}{|\overrightarrow{c}|sinB}(\overrightarrow{c}+\overrightarrow{b})$;
D在BC上;
∴$\overrightarrow{AD}=\frac{1}{2}\overrightarrow{c}+\frac{1}{2}\overrightarrow{b}$.
故选:B.
点评 考查正弦定理,以及向量加法的平行四边形法则,向量的数乘运算.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目