题目内容
3.设数列{an}的前n项和为Sn,对一切n∈N+,点(n,$\frac{{S}_{n}}{n}$)均在函数f(x)=3x+2的图象上.(1)求a1,a2及数列{an}的通项公式;
(2)解不等式f(n)≥Sn-22.
分析 (1)由点(n,$\frac{{S}_{n}}{n}$)均在函数f(x)=3x+2的图象上,可得${S}_{n}=3{n}^{2}+2n$,分别取n=1,2求得a1,a2,再由an=Sn-Sn-1(n≥2)求得数列{an}的通项公式;
(2)求出f(n),代入f(n)≥Sn-22,求解关于n的一元二次不等式得答案.
解答 解:(1)由(n,$\frac{{S}_{n}}{n}$)在函数f(x)=3x+2的图象上,
得$\frac{{S}_{n}}{n}=3n+2$,
∴${S}_{n}=3{n}^{2}+2n$,
则a1=S1=5,${a}_{1}+{a}_{2}=3×{2}^{2}+2×2=16$,
∴a2=11,
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}=3{n}^{2}+2n$-[3(n-1)2+2(n-1)]=6n-1;
(2)由f(n)≥Sn-22,
得3n+2≥3n2+2n-22,
即3n2-n-24≤0,
解得:$-\frac{8}{3}≤n≤3$,
∵n∈N+,
∴n=1,2,3.
则不等式f(n)≥Sn-22的解集为{1,2,3}.
点评 本题考查数列递推式,考查了等差数列的通项公式,训练了一元二次不等式的解法,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13.已知数列{an}的前n项和Sn=2n+t(t是实常数),下列结论正确的是( )
| A. | t为任意实数,{an}均是等比数列 | B. | 当且仅当t=-1时,{an}是等比数列 | ||
| C. | 当且仅当t=0时,{an}是等比数列 | D. | 当且仅当t=-2时,{an}是等比数列 |
11.若直线a平行于平面β,点A∈a,则过点A且平行于平面β的直线( )
| A. | 只有一条,但不一定在平面β内 | B. | 只有一条,一定在平面β内 | ||
| C. | 有无数条,但都不在平面β内 | D. | 有无数条,都在平面β内 |
8.在数列{an}中,a1=3,an+1=3${a}_{n}^{2}$(n∈N*),数列{bn}满足bn=log3an,数列{bn}的前n项和为Tn,若2Tn>2013,则n的最小值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
12.在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点D在BC边上且$\overrightarrow{AD}$=λ($\frac{c}{|c|sinB}+\frac{b}{|b|sinC}$)(λ∈R),则( )
| A. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\overrightarrow{b}$ | B. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{c}$-$\overrightarrow{b}$ |
13.某协会举办行业知识测试,为更好地了解从业人员对行业知识掌握程度的分布情况,从参加测试的人中随机抽取100人,对他们的行业测试成绩进行统计,得到如下频数分布表:
依此数据,估计这次行业知识测试的平均成绩$\overline{x}$和方差s2.
| 成绩 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 10 | 20 | 35 | 30 | 5 |
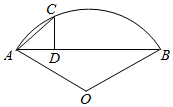 如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.
如图,若$\widehat{ACB}$是半径为r的圆的弓形,弦AB长为$\sqrt{2}$r,C为劣弧AB上的一点,CD⊥AB于D,当点C在什么位置时,△ACD的面积最大,并求这个最大面积.