题目内容
3.在锐二面角α-AB-β的面α内一点P到β的距离为P到棱AB的距离的一半,求此二面角的大小.分析 根据条件作出二面角的平面角,结合直角三角形中的边角关系进行求解即可.
解答 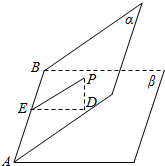 解:如图,∵二面角α-AB-β的平面角是锐角θ,
解:如图,∵二面角α-AB-β的平面角是锐角θ,
过P作PD⊥β,
平面α内有一点C到β的距离为3,
点C到棱AB距离为4,
作PE⊥AB,连接ED,
则PD⊥AB,
则AB⊥面PED,
则DE⊥AB,
则∠PED=θ,
∵P到β的距离为P到棱AB的距离的一半,
∴PE=2PD,
在直角三角形PDE中,sinθ=$\frac{PD}{PE}=\frac{PE}{2PE}=\frac{1}{2}$,
则θ=30°,
即二面角α-AB-β的大小为30°.
点评 本题主要考查了空间二面角的求解,根据定义作出二面角的平面角是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一位母亲记录了儿子3-9岁的身高,收集了好几组数据(略),由此建立的身高与年龄的回归模型为y=7.18x+73.95,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A. | 身高在145.75cm以上 | B. | 身高在145.75cm左右 | ||
| C. | 身高一定是145.75cm | D. | 身高在145.75cm以下 |
18.p:5是15的约数; q:π是有理数 则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ¬p是真命题 | D. | ¬q是真命题 |
12.已知集合A={x∈Z||x|<4},B={x|x-1≥0},则A∩B等于( )
| A. | (1,4) | B. | [1,4) | C. | {1,2,3} | D. | {2,3,4} |

 如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.