题目内容
11. 如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.(1)证明:平面PCE⊥平面PAB;
(2)证明:MN∥平面PAC;
(3)若∠PAC=60°,求二面角P-CE-A的大小.
分析 (1)根据面面垂直的性质定理证明平面PCE⊥平面PAB.
(2)根据面面平行的性质定理证明平面MNF∥平面PAC,即可证明MN∥平面PAC;
(3)建立空间直角坐标系,求出对应平面的法向量,利用向量法进行求解即可.
解答  证明:(1)∵∠APC=90°,∴PC⊥AP,
证明:(1)∵∠APC=90°,∴PC⊥AP,
∵AB⊥平面PAC,PC?平面PAC,
∴AB⊥PC,
∵AP∩AB=A,
∴PC⊥平面PAB,
∵PC?平面PCE,
∴平面PCE⊥平面PAB;
(2)取AE的中点F,连接FN,FM,
∵M是CE的中点,∴MF是△AEC的中位线,
则MF∥AC,AB=2AE=4AF
∵4PN=PB,
∴PB:PN=AB:AF,则FN∥AP,
∵AP∩PC=C,∴平面MNF∥平面PAC;
∵MN?面MNF;
∴MN∥平面PAC,
(3)过P作PO⊥AC于O,则PO⊥平面ABC,过O作AB的平行线交BC于H,
以O坐标原点建立空间坐标系如图:
若∠PAC=60°,
∵∠APC=90°,AB=1,AC=$\sqrt{2}$,E是AB的中点,M是CE的中点,
∴AP=$\frac{1}{2}AC$=$\frac{\sqrt{2}}{2}$,OA=$\frac{1}{2}$AP=$\frac{\sqrt{2}}{4}$,OC=AC-OA=$\sqrt{2}-\frac{\sqrt{2}}{4}$=$\frac{3\sqrt{2}}{4}$.
OP=APsin60°=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{4}$,AE=$\frac{1}{2}$,
则A($\frac{\sqrt{2}}{4}$,0,0),E($\frac{\sqrt{2}}{4}$,$\frac{1}{2}$,0),C(-$\frac{3\sqrt{2}}{4}$,0,0),P(0,0,$\frac{\sqrt{6}}{4}$),
则平面AEC的一个法向量为$\overrightarrow{m}$=(0,0,1),
设平面PEC的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{CE}$=($\sqrt{2}$,$\frac{1}{2}$,0),$\overrightarrow{PC}$=(-$\frac{3\sqrt{2}}{4}$,0,-$\frac{\sqrt{6}}{4}$),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CE}=0}\\{\overrightarrow{n}•\overrightarrow{PC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\sqrt{2}x+\frac{1}{2}y=0}\\{-\frac{3\sqrt{2}}{4}x-\frac{\sqrt{6}}{4}z=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{y=-2\sqrt{2}z}\\{z=-\sqrt{3}x}\end{array}\right.$,令x=1,则z=-$\sqrt{3}$,y=2$\sqrt{2}$,
即$\overrightarrow{n}$=(1,2$\sqrt{2}$,-$\sqrt{3}$),则|$\overrightarrow{n}$|=$\sqrt{1+8+3}$=2$\sqrt{3}$,
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-\sqrt{3}}{2\sqrt{3}}$═-$\frac{1}{2}$,
即<$\overrightarrow{m}$,$\overrightarrow{n}$>=120°,
∵二面角P-CE-A是锐二面角,
∴二面角P-CE-A的大小为60°.
点评 本题综合考查空间中面面垂直,线面平行的判断和空间角的计算,涉及二面角的平面角,利用向量法是解决空间角常用的方法,考查的知识面较广,综合性较强,运算量较大.

 阅读快车系列答案
阅读快车系列答案
| A. | 36 | B. | 40 | C. | 44 | D. | 48 |
| A. | {2} | B. | {3} | C. | {2,3} | D. | {1,2,4} |
| A. | ($\frac{p}{2}$,0) | B. | (p,0) | C. | (2p,0) | D. | (3p,0) |
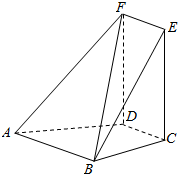 如图,在多面体EF-ABCD中,四边形ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,四边形DCEF为平行四边形,平面DCEF⊥平面ABCD.
如图,在多面体EF-ABCD中,四边形ABCD,ABEF均为直角梯形,∠ABE=∠ABC=$\frac{π}{2}$,四边形DCEF为平行四边形,平面DCEF⊥平面ABCD. 函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论: