题目内容

13．设f（x）=（x-3）（x-2）（x-1）x（x+1）（x+2）（x+3），则f'（0）=-36．

分析 将函数f（x）分组，根据导数运算法则，即可求得f（x）的导函数，当x=0时，代入即可求得f'（0）．

解答 解：f（x）=（x-3）（x-2）（x-1）x（x+1）（x+2）（x+3）
=x（x-3）（x-2）（x-1）（x+1）（x+2）（x+3），
求导f′（x）=（x）′（x-3）（x-2）（x-1）（x+1）（x+2）（x+3）+x[（x-3）（x-2）（x-1）（x+1）（x+2）（x+3）]′，
=（x-3）（x-2）（x-1）（x+1）（x+2）（x+3）+x[（x-3）（x-2）（x-1）（x+1）（x+2）（x+3）]′，
f′（0）=（0-3）（0-2）（0-1）（0+1）（0+2）（0+3）+0×[（x-3）（x-2）（x-1）（x+1）（x+2）（x+3）]′，
=-36，
故答案为：-36．

点评 本题考查导数的运算，导数的求得法则，采用分组求导数法，观察所求导数，构造出含有零项，考查计算能力，属于基础题．

练习册系列答案
相关题目
3．已知函数f（x）=$\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2}$，x∈R．
（Ⅰ） 求函数f（x）的最小值和最小正周期；
（2）求函数f（x），x∈[0，π]单调递减区间．
4．已知函数f（x）=logax（a＞0，a≠1），且f（4）-f（2）=1．
（1）若f（3m-3）＜f（2m+1），求实数m的取值范围；
（2）求使$f（x+\frac{2}{x}）={log_2}3$成立的x的值．
1．已知复数z=$\frac{4-3i}{6+8i}$（i是虚数单位），则|z|=（　　）
A．$\frac{1}{2}$B．1C．$\frac{7}{48}$D．$\frac{3}{10}$
8．若（x2-3x+2）5=${a_0}+{a_1}x+{a_2}{x^2}+{a_3}{x^3}+…+{a_{10}}{x^{10}}$
（1）求a2
（2）求a1+a2+a3+…+a10
（3）求$（{a_0}+{a_2}+{a_4}+{a_6}+{a_8}{+_{10}}{）^2}$-$（{a_1}+{a_3}+{a_5}+{a_7}+{a_9}{）^2}$．
2．证明：函数f（x）=cos2x+cos2（x+$\frac{π}{3}$）+cos2（x-$\frac{π}{3}$）是常数函数．
9．设直线x=m分别交函数$y=sinx、y=sin（x+\frac{π}{2}）$的图象于M、N、两点，则M、N距离的最大值为（　　）
A．1B．$\sqrt{2}$C．2D．2$\sqrt{2}$
6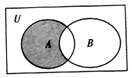．若全集U、集合A、集合B及其关系用韦恩图表示如图所示，则图中阴影表示的集合为（　　）
A．∁U（A∩B）B．∁U（A∪B）C．A∩（∁UB）D．（∁UA）∩B
7．（1）若（$\frac{1}{2}$+2x）n的展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项的系数；
（2）（a+x）（a+x）4的展开式中x的奇数次幂项的系数之和为32，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网