题目内容
8.若x,y满足约束条件$\left\{\begin{array}{l}x+y-5≤0\\ 2x-y-1≥0\\ x-2y+1≤0\end{array}\right.$,则2x-3y的最小值为-5.分析 首先画出可行域,关键目标函数的几何意义求最小值.
解答  解:由约束条件得到可行域如图:z=2x-3y变形为y=$\frac{2}{3}$x-$\frac{z}{3}$,
解:由约束条件得到可行域如图:z=2x-3y变形为y=$\frac{2}{3}$x-$\frac{z}{3}$,
当此直线经过图中A时,在y轴的截距最大,z最小,
由$\left\{\begin{array}{l}{2x-y-1=0}\\{x+y-5=0}\end{array}\right.$,解得A(2,3)
所以z的最小值为2×2-3×3=-5;
故答案为:-5.
点评 本题考查了简单线性规划问题;正确画出可行域,利用目标函数的几何意义求最值是常规方法.

练习册系列答案
相关题目
18.有5件不同的商品,其中2件次品,3件正品,从中取出2件,至少有1件次品的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
16.设A是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右顶点,F(c,0)是右焦点,若抛物线${y^2}=-\frac{{4{a^2}}}{c}x$的准线l上存在一点P,使∠APF=30°,则双曲线的离心率的范围是( )
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
13.已知等比数列{an}的前n项和Sn=2n-a,则数列{log2an}的前10项和等于( )
| A. | 1023 | B. | 55 | C. | 45 | D. | 35 |
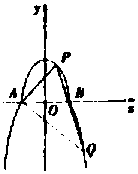 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.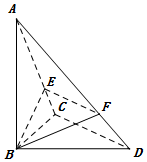 在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.