题目内容
3.定义在R上的函数f(x)满足$f(x)=\left\{\begin{array}{l}{{3}^{x-1},x≤0}\\{f(-x+3),x>0}\end{array}\right.$,则f(2016)=$\frac{1}{3}$.分析 由已知条件利用分段函数的性质直接求解.
解答 解:∵定义在R上的函数f(x)满足$f(x)=\left\{\begin{array}{l}{{3}^{x-1},x≤0}\\{f(-x+3),x>0}\end{array}\right.$,
∴f(2016)=f(-2016+3×672)=f(0)=30-1=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
相关题目
8.下列命题正确的是( )
| A. | 命题:若x=3,则x2-2x-3=0的否命题是:若x≠3,则x2-2x-3≠0 | |
| B. | 命题:?x∈R,使得x2-1<0的否定是:?x∈R,均有x2-1<0 | |
| C. | 命题:存在四边相等的四边形不是正方形,该命题是假命题 | |
| D. | 命题:cosx=cosy,则x=y的逆否命题是真命题 |
13.一个均匀的正方体玩具的各个面上分别标有数字1,2,3,4,5,6,将这个玩具向上抛掷一次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过2,事件C表示向上的一面出现的点数不小于4,则( )
| A. | A与B是互斥而非对立事件 | B. | A与B是对立事件 | ||
| C. | B与C是互斥而非对立事件 | D. | B与C是对立事件 |
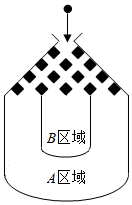 如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
如图,将一个半径适当的小球放入容器上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物3次,最后落入A区域或B区域中,已知小球每次遇到障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$. 对于实数a和b,定义运算a*b,运算原理如图所示,若(1+m)*(1-m)=2,则实数m=0,或1,或-1.
对于实数a和b,定义运算a*b,运算原理如图所示,若(1+m)*(1-m)=2,则实数m=0,或1,或-1.