题目内容
已知函数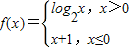
，若f（a）=2，则a=（ ）A．4
B．2
C．1
D．-1
【答案】分析：由函数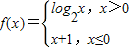
，f（a）=2，知当a＞0时，f（a）=log2a=2，当a≤0时，f（a）=a+1=2，由此能求出结果．
解答：解：∵函数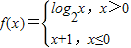
，f（a）=2，
∴当a＞0时，f（a）=log2a=2，a=22=4；
当a≤0时，f（a）=a+1=2，a=1（舍）．
故a=4．
故选A．
点评：本题考查函数值的求法和应用，是基础题．解题时要认真审题，仔细解答．
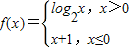，f（a）=2，知当a＞0时，f（a）=log2a=2，当a≤0时，f（a）=a+1=2，由此能求出结果．解答：解：∵函数
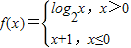，f（a）=2，∴当a＞0时，f（a）=log2a=2，a=22=4；
当a≤0时，f（a）=a+1=2，a=1（舍）．
故a=4．
故选A．
点评：本题考查函数值的求法和应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
相关题目
，若f（a﹣2）+f（a）＞0，则实数a的取值范围是（ ）
或
或
，若f（a）=2，则a= ．
，若f（a）=2，则a= ．
，若f（a）＞f（-a），求实数a的取值范围．
，若f（a）=-1，则a=（ ）