题目内容
已知函数 ,若f(a)>f(-a),求实数a的取值范围.
,若f(a)>f(-a),求实数a的取值范围.
【答案】分析:通过对a>0与a<0,利用分段函数,写出f(a)>f(-a),利用对数的性质,求出a的范围即可.
解答:解:当a>0时,由f(a)>f(-a)得 >
> ,即
,即 >-
>- ,可得:a>1;
,可得:a>1;
当a<0时,同样得 >
> ,即-
,即- >
> .可得:-1<a<0;
.可得:-1<a<0;
综上得:-1<a<1或a>1.
所求a的范围是:(-1,0)∪(1,+∞)
点评:本题考查分段函数的解析式的应用,对数函数的基本性质,考查计算能力.
解答:解:当a>0时,由f(a)>f(-a)得
 >
> ,即
,即 >-
>- ,可得:a>1;
,可得:a>1;当a<0时,同样得
 >
> ,即-
,即- >
> .可得:-1<a<0;
.可得:-1<a<0;综上得:-1<a<1或a>1.
所求a的范围是:(-1,0)∪(1,+∞)
点评:本题考查分段函数的解析式的应用,对数函数的基本性质,考查计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
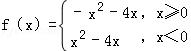 ,若f(a﹣2)+f(a)>0,则实数a的取值范围是( )
,若f(a﹣2)+f(a)>0,则实数a的取值范围是( ) ,若f(a)=2,则a= .
,若f(a)=2,则a= . ,若f(a)=2,则a= .
,若f(a)=2,则a= . ,若f(a)=-1,则a=( )
,若f(a)=-1,则a=( )