题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() .过
.过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 位于第一象限,且
位于第一象限,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由![]() 的周长为
的周长为![]() 得
得![]() ,再结合
,再结合![]() 即可解出a,b;
即可解出a,b;
(2)设![]() ,由
,由![]() 得
得![]() ,联立椭圆方程可解得A点坐标,然后再写出直线
,联立椭圆方程可解得A点坐标,然后再写出直线![]() 的方程,联立椭圆方程得到B点坐标即可解决.
的方程,联立椭圆方程得到B点坐标即可解决.
解:(1)因为椭圆![]() 的离心率
的离心率![]() ,
,
所以![]() ①.
①.
又![]() 的周长为
的周长为![]() ,所以
,所以![]() .②
.②
联立①②,解得![]() ,从而
,从而![]() ,
,
因此椭圆![]() 的方程为
的方程为![]() .
.
(2)因为点![]() 位于第一象限,故设
位于第一象限,故设![]() ,其中
,其中![]() .
.
因为![]() ,所以
,所以![]() ,又点
,又点![]() 在椭圆
在椭圆![]() 上,
上,
所以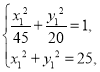 解得
解得![]() ,从而
,从而![]() .
.
由(1)知,椭圆![]() 的左焦点为
的左焦点为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
由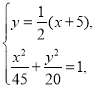 得
得![]() ,解得
,解得![]() 或
或![]() .
.
所以![]() .
.
因为![]() ,所以
,所以![]() 的外接圆就是以
的外接圆就是以![]() 为直径的圆.
为直径的圆.
又椭圆![]() 的右焦点为
的右焦点为![]() ,
,
所以线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,此时
,此时![]() ,
,
故![]() 的外接圆的方程为
的外接圆的方程为![]() .
.

练习册系列答案
相关题目