题目内容
【题目】已知函数![]() .
.
(1)当![]() 时.
时.
①求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②定义![]() 其中
其中![]() ,求
,求![]() ;
;
(2)当![]() 时,设
时,设![]() ,
,![]() (
(![]() 为自然对数的底数),若对任意给定的
为自然对数的底数),若对任意给定的![]() ,在
,在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②8079;(2)
;②8079;(2)![]() .
.
【解析】
(1)①![]() 时,
时,![]() ,
,![]() ,利用导数的几何意义能求出函数
,利用导数的几何意义能求出函数![]() 在
在![]() 处的切线方程.
处的切线方程.
②由![]() ,得
,得![]() ,由此能求出
,由此能求出![]() 的值.
的值.
(2)根据若对任意给定的![]() ,
,![]() ,在区间
,在区间![]() ,
,![]() 上总存在两个不同的
上总存在两个不同的![]() ,使得
,使得![]() 成立,得到函数
成立,得到函数![]() 在区间
在区间![]() ,
,![]() 上不单调,从而求得
上不单调,从而求得![]() 的取值范围.
的取值范围.
(1)①∵![]() ,
,![]()
∴![]()
∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
所以切线方程为![]() .
.
②![]() ,
,![]()
![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
因为![]() ①,
①,
所以![]() ②,
②,
由①+②得![]() ,所以
,所以![]() .
.
所以![]() .
.
(2)![]() ,当
,当![]() 时,
时,![]() 函数
函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减∵
单调递减∵![]() ,
,![]() ,
,![]()
所以,函数![]() 在
在![]() 上的值域为
上的值域为![]() .
.
因为![]() ,
,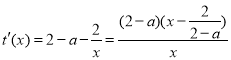 ,
,![]()
故![]() ,
,![]() ,①
,①
此时,当![]() 变化时
变化时![]() 、
、![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
| — | 0 | + |
| 单调减 | 最小值 | 单调增 |
∵![]() ,
,![]()
![]() ,
,![]()
∴对任意给定的![]() ,在区间
,在区间![]() 上总存在两个不同的
上总存在两个不同的![]() ,
,
使得![]() 成立,当且仅当
成立,当且仅当![]() 满足下列条件
满足下列条件
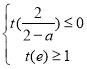 ,即
,即
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,函数
,函数![]() 单调递减所以,对任意
单调递减所以,对任意![]() ,有
,有![]() ,即②对任意
,即②对任意![]() 恒成立.
恒成立.
由③式解得:![]() ④
④
综合①④可知,当![]() 时,对任意给定的
时,对任意给定的![]() ,
,
在![]() 上总存在两个不同的
上总存在两个不同的![]() ,使
,使![]() 成立.
成立.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目