题目内容
15.飞机沿水平方向飞行,在A处测得正前下方地面目标C的俯角为30°,向前飞行10000米到达B处,此时测得正前下方目标C的俯角为75°,这时飞机与地面目标的水平距离为( )| A. | 2500($\sqrt{3}-1$)米 | B. | 5000$\sqrt{2}$米 | C. | 4000米 | D. | 4000$\sqrt{2}$米 |
分析 在△ABC中,使用正弦定理求出BC,则飞机与地面目标的水平距离为BCcos75°.
解答 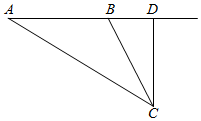 解:过C作CD⊥AB交AB的延长线于D,由题意得A=30°,∠CBD=75°,AB=10000m,
解:过C作CD⊥AB交AB的延长线于D,由题意得A=30°,∠CBD=75°,AB=10000m,
∴∠ABC=105°,∠ACB=180°-A-∠ABC=45°,
在△ABC中,由正弦定理得$\frac{AB}{sin∠ACB}=\frac{BC}{sinA}$,即$\frac{10000}{\frac{\sqrt{2}}{2}}=\frac{BC}{\frac{1}{2}}$,
解得BC=5000$\sqrt{2}$.
∴BD=BC•cos∠CBD=5000$\sqrt{2}×$cos75°=5000$\sqrt{2}$×$\frac{\sqrt{6}-\sqrt{2}}{4}$=2500($\sqrt{3}-1$).
故选:A.
点评 本题考查了解三角形的实际应用,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=x2+2x(x>0),f1(x)=f(x),fn+1(x)=f(fn(x)),n∈N*,则f5(x)在[1,2]上的最大值是( )
| A. | 210-1 | B. | 232-1 | C. | 310-1 | D. | 332-1 |



