题目内容
13．已知点（a，b）是平面区域$\left\{\begin{array}{l}{x+y-2≤0}\\{x≥0}\\{y≥-1}\end{array}\right.$内的任意一点，则3a-b的最小值为（ ）| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
分析 作出不等式组对应的平面区域，利用z的几何意义，结合数形结合即可得到结论．
解答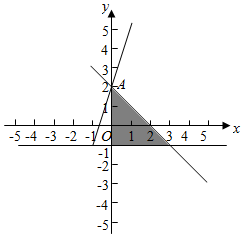 
解：作出不等式组对应的平面区域如图：
点（a，b）是平面区域$\left\{\begin{array}{l}{x+y-2≤0}\\{x≥0}\\{y≥-1}\end{array}\right.$内的任意一点，
由z=3a-b得b=3a-z，
平移直线y=3x-z由图象可知当直线y=3x-z经过点A时，
直线y=3x-z的截距最大，
此时z最小．
由$\left\{\begin{array}{l}{x=0}\\{x+y=2}\end{array}\right.$，解得A（0，2），
此时z=3×0-2=-2，
故选：B．
点评 本题主要考查线性规划的应用，利用z的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
1．一个正项等比数列前n项的和为3，前3n项的和为21，则前2n项的和为（ ）
| A． | 18 | B． | 12 | C． | 9 | D． | 6 |
8．下列说法错误的是（ ）
| A． | 命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0” | |
| B． | 如果命题“￢p”与命题“p∨q”都是真命题，则命题q一定是真命题 | |
| C． | 若命题：?x0∈R，${x_0}^2-{x_0}+1＜0$，则￢p：?x∈R，x2-x+1≥0 | |
| D． | “$sinθ=\frac{1}{2}$”是“$θ=\frac{π}{6}$”的充分不必要条件 |
7．三角形的面积$s=\frac{1}{2}（a+b+c）r$，a﹑b﹑c 为三边的边长，r为三角形内切圆半径，利用类比推理可以得到四面体的体积为（ ）
| A． | V=$\frac{1}{3}$abc | |
| B． | $V=\frac{1}{3}sh$ | |
| C． | $V=\frac{1}{3}（ab+bc+ca）h$ | |
| D． | $V=\frac{1}{3}（{s_1}+{s_2}+{s_3}+{s_4}）r$（s1，s2，s3，s4分别为四个面的面积，r为四面体内切球半径） |