题目内容
18.在△ABC中,角A,B,C的对边分别为a,b,c.已知a=2,c=$\sqrt{2}$,cosA=-$\frac{{\sqrt{2}}}{4}$.则b的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
分析 由题意和同角三角函数基本关系可得sinA,再由正弦定理可得sinC,进而可得cosC,可得cosB,由余弦定理可得.
解答 解:∵在△ABC中a=2,c=$\sqrt{2}$,cosA=-$\frac{{\sqrt{2}}}{4}$,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{14}}{4}$,
由正弦定理可得sinC=$\frac{csinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{14}}{4}}{2}$=$\frac{\sqrt{7}}{4}$,
∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{3}{4}$,
∴cosB=-cos(A+C)=sinAsinC-cosAcosC
=$\frac{\sqrt{14}}{4}$×$\frac{\sqrt{7}}{4}$-(-$\frac{{\sqrt{2}}}{4}$)×$\frac{3}{4}$=$\frac{5\sqrt{2}}{8}$,
∴由余弦定理可得b=$\sqrt{4+2-2×2×\sqrt{2}×\frac{5\sqrt{2}}{8}}$=1,
故选:A.
点评 本题考查正余弦定理解三角形,涉及同角三角函数基本关系和和差角的三角函数公式,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设数列{an}各项均为正值,且前n项和Sn=$\frac{1}{2}$(an+$\frac{1}{{a}_{n}}$),则此数列的通项an应为( )
| A. | an=$\sqrt{n+1}$-$\sqrt{n}$ | B. | an=$\sqrt{n}$-$\sqrt{n-1}$ | C. | an=$\sqrt{n+2}$-$\sqrt{n+1}$ | D. | an=2$\sqrt{n}$-1 |
3.一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,从袋中随机取出两个球,则取出的球的编号之和不大于4的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
10.i为虚数单位,z=$\frac{5i}{1+2i}$,则|$\overline{z}$|=( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 1 | D. | 2 |
7.若cos2x>sin2x,x∈[0,π],则x的取值范围是( )
| A. | [0,$\frac{π}{4}$)∪[$\frac{π}{2}$,$\frac{3}{4}$π] | B. | [0,$\frac{π}{4}$)∪($\frac{3}{4}π$,π] | C. | [0,$\frac{π}{4}$)∪($\frac{π}{2}$,$\frac{3}{4}$π] | D. | [$\frac{π}{2}$,π] |
8.将函数f(x)=cos(2x+$\frac{π}{6}$)的图象沿x向右平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,若P(x0,$\frac{1}{2}$)是函数y=g(x)的图象上一点,则sin($\frac{2π}{3}$-2x0)=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{\sqrt{3}}{2}$ |
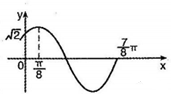 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则此函数的解析式为f(x)=2sin(2x+$\frac{π}{4}$).