题目内容
19.设函数f(x)=lnx,g(x)=lnx-x+2.(1)求函数g(x)的极大值;
(2)若关于x的不等式$mf(x)≥\frac{x-1}{x+1}$在[1,+∞)上恒成立,求实数m的取值范围;
(3)已知$α∈(0,\frac{π}{2})$,试比较f(tanα)与-cos2α的大小,并说明理由.
分析 (1)求出g(x)的导数,得到g(x)的单调区间,从而求出g(x)的极大值即可;
(2)问题转化为mlnx-$\frac{x-1}{x+1}$≥0,令h(x)=mlnx-$\frac{x-1}{x+1}$,求出函数h(x)的导数,根据函数的单调性求出m的范围即可;
(3)令F(a)=ln(tana)+cos2a,求出函数F(a)的导数,根据a的范围,求出函数的单调性,从而比较f(tana)和-cos2a的大小即可.
解答 解:(1)∵g(x)=lnx-x+2,(x>0),则g′(x)=$\frac{1-x}{x}$,
当x∈(0,1)时,g′(x)>0,当x∈(1,+∞)时,g′(x)<0,
∴g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴当x=1时,函数g(x)取得极大值1.
(2)mf(x)≥$\frac{x-1}{x+1}$?mlnx-$\frac{x-1}{x+1}$≥0,
令h(x)=mlnx-$\frac{x-1}{x+1}$,则h′(x)=$\frac{{m(x+1)}^{2}-2x}{{x(x+1)}^{2}}$,
∵h(1)=0,故当m(x+1)2-2x≥0[1,+∞)在上恒成立时,
使得函数h(x)在[1,+∞)上单调递增,
∴m≥$\frac{2x}{{(x+1)}^{2}}$=$\frac{2}{x+\frac{1}{x}+2}$在[1,+∞)上恒成立,故m≥$\frac{1}{2}$;
经验证,当m≥$\frac{1}{2}$时,函数h′(x)≥0在[1,+∞)上恒成立;
当m<$\frac{1}{2}$时,不满足题意.
∴m≥$\frac{1}{2}$.
(3)令F(α)=ln(tanα)+cos2α,则F′(α)=$\frac{2(1{-sin}^{2}2α)}{sin2α}$,
∵α∈(0,$\frac{π}{2}$),∴sin2α>0,∴F′(α)>0,
故F(α)单调递增,又F($\frac{π}{4}$)=0,
∴当0<α<$\frac{π}{4}$时,f(tanα)<-cos2α;
当α=$\frac{π}{4}$时,f(tanα)=-cos2α;
当$\frac{π}{4}$<α<$\frac{π}{2}$,f(tanα)>-cos2α.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

| A. | (0,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [2,4] |
| A. | {x|0<x<3} | B. | {x|0<x<5} | C. | {x|3<x<5} | D. | {x|x<0} |
| A. | 43<33 | B. | log0.54<log0.56 | C. | ($\frac{1}{2}$)-3>($\frac{1}{2}$)3 | D. | lg1.6<lg1.4 |
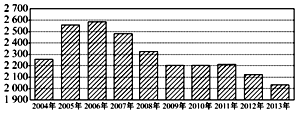 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )| A. | 逐年比较,2005年减少二氧化硫排放量的效果最显著 | |
| B. | 2008年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
| A. | (1,2) | B. | ($\frac{1}{e}$,1) | C. | (2,3) | D. | (e,+∞) |