题目内容
过点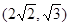 的双曲线
的双曲线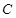 的渐近线方程为
的渐近线方程为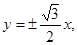
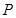 为双曲线
为双曲线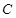 右支上一点,
右支上一点,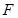 为双曲线
为双曲线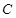 的左焦点,点
的左焦点,点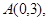 则
则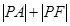 的最小值为 .
的最小值为 .
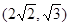 的双曲线
的双曲线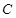 的渐近线方程为
的渐近线方程为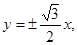
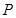 为双曲线
为双曲线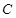 右支上一点,
右支上一点,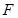 为双曲线
为双曲线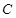 的左焦点,点
的左焦点,点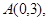 则
则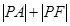 的最小值为 .
的最小值为 .8
试题分析:由题可设双曲线方程为:
 ,把
,把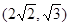 代入得
代入得 =1,所以双曲线方程为:
=1,所以双曲线方程为: ,
,设双曲线右焦点为
 ,∵P在双曲线右支上及由双曲线定义可知
,∵P在双曲线右支上及由双曲线定义可知 ,∴
,∴ ,当点P为线段
,当点P为线段 与双曲线交点时
与双曲线交点时 .
.
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
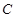 :
: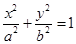
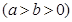 的离心率
的离心率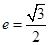 ,原点到过点
,原点到过点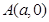 ,
,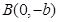 的直线的距离是
的直线的距离是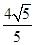 .
.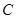 的方程;
的方程; 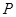
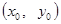 关于直线
关于直线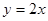 的对称点为
的对称点为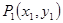 ,求
,求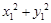 的取值范围;
的取值范围;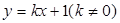 交椭圆
交椭圆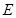 ,
,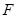 ,且
,且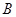 为圆心的圆上,求
为圆心的圆上,求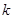 的值.
的值.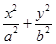 =1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+
=1(a>b>0)的离心率与等轴双曲线的离心率互为倒数关系,直线l:x-y+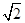 =0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.
=0与以原点为圆心, 以椭圆C的短半轴长为半径的圆相切.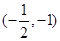 .
.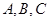 为椭圆
为椭圆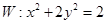 上的三个点,
上的三个点,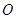 为坐标原点.
为坐标原点.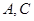 所在的直线方程为
所在的直线方程为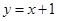 ,求
,求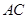 的长;
的长;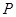 为线段
为线段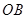 上一点,且
上一点,且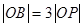 ,当
,当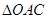 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.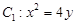 在点
在点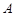 ,
,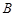 处的切线垂直相交于点
处的切线垂直相交于点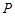 ,直线
,直线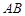 与椭圆
与椭圆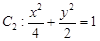 相交于
相交于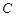 ,
,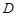 两点.
两点.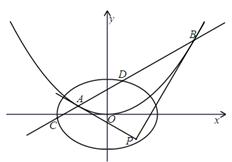
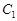 的焦点
的焦点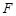 与椭圆
与椭圆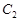 的左焦点
的左焦点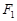 的距离;
的距离;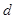 ,试问:是否存在直线
,试问:是否存在直线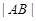 ,
,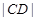 成等比数列?若存在,求直线
成等比数列?若存在,求直线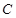 两焦点坐标分别为
两焦点坐标分别为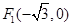 ,
,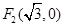 ,且经过点
,且经过点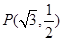 .
.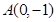 ,直线
,直线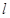 与椭圆
与椭圆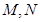 .若△
.若△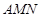 是以
是以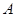 为直角顶点的等腰直角三角形,试求直线
为直角顶点的等腰直角三角形,试求直线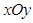 中,椭圆
中,椭圆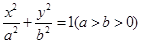 的离心率
的离心率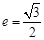 ,
,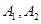 分别是椭圆的左、右两个顶点,圆
分别是椭圆的左、右两个顶点,圆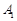 的半径为
的半径为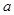 ,过点
,过点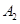 作圆
作圆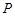 ,在
,在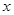 轴的上方交椭圆于点
轴的上方交椭圆于点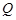 .则
.则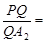 .
.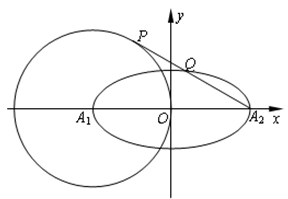
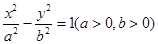 的顶点恰好是椭圆
的顶点恰好是椭圆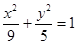 的两个顶点,且焦距是
的两个顶点,且焦距是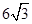 ,则此双曲线的渐近线方程是( )
,则此双曲线的渐近线方程是( )


