题目内容
如图平面直角坐标系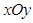 中,椭圆
中,椭圆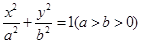 的离心率
的离心率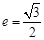 ,
,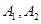 分别是椭圆的左、右两个顶点,圆
分别是椭圆的左、右两个顶点,圆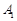 的半径为
的半径为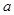 ,过点
,过点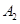 作圆
作圆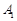 的切线,切点为
的切线,切点为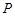 ,在
,在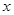 轴的上方交椭圆于点
轴的上方交椭圆于点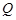 .则
.则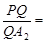 .
.
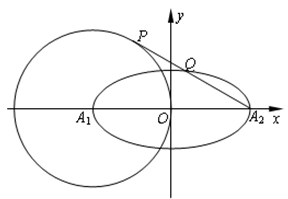
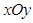 中,椭圆
中,椭圆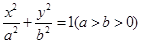 的离心率
的离心率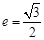 ,
,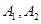 分别是椭圆的左、右两个顶点,圆
分别是椭圆的左、右两个顶点,圆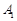 的半径为
的半径为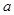 ,过点
,过点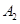 作圆
作圆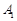 的切线,切点为
的切线,切点为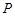 ,在
,在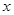 轴的上方交椭圆于点
轴的上方交椭圆于点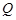 .则
.则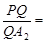 .
.

试题分析:因为
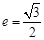 所以
所以 又直角三角形中
又直角三角形中 ,所以
,所以 ,直线
,直线 方程为
方程为 ,与椭圆方程
,与椭圆方程 联立方程组解得
联立方程组解得 ,又
,又 ,所以
,所以

练习册系列答案
相关题目
题目内容
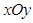 中,椭圆
中,椭圆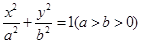 的离心率
的离心率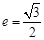 ,
,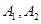 分别是椭圆的左、右两个顶点,圆
分别是椭圆的左、右两个顶点,圆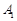 的半径为
的半径为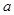 ,过点
,过点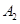 作圆
作圆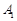 的切线,切点为
的切线,切点为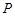 ,在
,在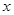 轴的上方交椭圆于点
轴的上方交椭圆于点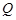 .则
.则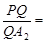 .
.

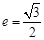 所以
所以 又直角三角形中
又直角三角形中 ,所以
,所以 ,直线
,直线 方程为
方程为 ,与椭圆方程
,与椭圆方程 联立方程组解得
联立方程组解得 ,又
,又 ,所以
,所以
