题目内容
已知x，y满足
，则z=x-y的最大值是 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：根据二元一次不等式组表示平面区域，画出不等式组表示的平面区域，由z=x-y得y=x-z，利用平移求出z最大值即可．
解答：
解：不等式对应的平面区域如图：（阴影部分）．
由z=x-y得y=x-z，平移直线y=x-z，
由平移可知当直线y=x-z，经过点B时，
直线y=x-z的截距最小，此时z取得最大值，
由
，得
，
即B（3，-3）代入z=x-y得z=3-（-3）=6，
即z=x-y的最大值是6，
故答案为：6．
解：不等式对应的平面区域如图：（阴影部分）． 由z=x-y得y=x-z，平移直线y=x-z，
由平移可知当直线y=x-z，经过点B时，
直线y=x-z的截距最小，此时z取得最大值，
由
|
|
即B（3，-3）代入z=x-y得z=3-（-3）=6，
即z=x-y的最大值是6，
故答案为：6．
点评：本题主要考查线性规划的应用，利用图象平行求得目标函数的最大值和最小值，利用数形结合是解决线性规划问题中的基本方法．
练习册系列答案
名校课堂系列答案
相关题目
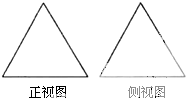如图是两个全等的正三角形，给定下列三个命题：①存在四棱锥，其正视图、侧视图如图；②存在三棱锥，其正视图、侧视图如图；③存在圆锥，其正视图、侧视图如图．其中真命题的个数是（ ）