题目内容
11.在等比数列{an}中,若a1=1,a4=27.(1)求a3.
(2)求数列通项公式an.
(3)求数列{an}的前n项的和Sn.
分析 由等比数列的通项公式求出公比和首项,由此能求出a3、数列通项公式an和数列{an}的前n项的和Sn.
解答 解:(1)∵在等比数列{an}中,若a1=1,a4=27,
∴${a}_{4}=1×{q}^{3}=27$,解得q=3,
∴a3=1×q2=9.
(2)${a}_{n}=1×{q}^{n-1}$=3n-1.
(3)${S}_{n}=\frac{1-{q}^{n}}{1-q}$=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}({3}^{n}-1)$.
点评 本题考查等比数列的第三项、通项公式和前n项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
3.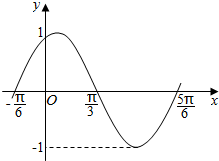 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )| A. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 |
1.已知函数$f(x)={log_a}({x^2}+2x-3)$,若f(2)<0,则此函数的单调递增区间是( )
| A. | (1,+∞)∪(-∞,-3) | B. | (1,+∞) | C. | (-∞,-1) | D. | (-∞,-3) |
 的内角
的内角 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、 ,已知
,已知 ,且
,且 .
. 的大小;
的大小; 与
与 共线, 求
共线, 求 的值.
的值.