题目内容
在△ABC中,已知
=
,求△ABC的形状.
| sin2A+sin2B-sin2C |
| sin2A-sin2B+sin2C |
| 1+cos2C |
| 1+cos2B |
∵
=
,
∴根据正弦定理与二倍角的余弦公式,得
=
∵a2+b2-c2=2abcosC,a2-b2+c2=2accosB,
∴代入,化简得
(
-
)=0,即
=0或
-
=0
①当
=0时,cosC=0得C=90°
②当
-
=0时,根据正弦定理得
-
=0
化简得sinBcosB=sinCcosC,即sin2B=sin2C
∴B=C或B+C=90°,三角形为等腰或直角三角形
综上所述,△ABC为等腰三角形或直角三角形.
| sin2A+sin2B-sin2C |
| sin2A-sin2B+sin2C |
| 1+cos2C |
| 1+cos2B |
∴根据正弦定理与二倍角的余弦公式,得
| a2+b2-c2 |
| a2-b2+c2 |
| cos2C |
| cos2B |
∵a2+b2-c2=2abcosC,a2-b2+c2=2accosB,
∴代入,化简得
| cosC |
| cosB |
| b |
| c |
| cosC |
| cosB |
| cosC |
| cosB |
| b |
| c |
| cosC |
| cosB |
①当
| cosC |
| cosB |
②当
| b |
| c |
| cosC |
| cosB |
| sinB |
| sinC |
| cosC |
| cosB |
化简得sinBcosB=sinCcosC,即sin2B=sin2C
∴B=C或B+C=90°,三角形为等腰或直角三角形
综上所述,△ABC为等腰三角形或直角三角形.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
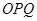 是半径为1,圆心角为
是半径为1,圆心角为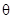 的扇形,
的扇形,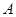 是扇形弧
是扇形弧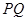 上的动点,
上的动点,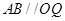 ,
,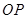 与
与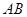 交于点
交于点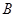 ,
,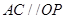 ,
,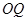 与
与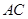 交于点
交于点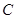 .记
.记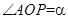 .
.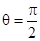 ,如图3,当角
,如图3,当角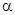 取何值时,能使矩形
取何值时,能使矩形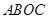 的面积最大;
的面积最大; ,如图4,当角
,如图4,当角
 ,则
,则 等于( )
等于( )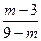




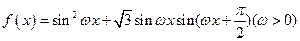 的最小正周期为
的最小正周期为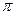 ,
,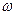 的值;(2)求函数
的值;(2)求函数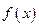 在区间
在区间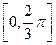 上的取值范围.
上的取值范围.