题目内容
已知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成角的余弦值为
A. | B. | C. | D. |
C
试题分析:由于是正方体,又是求角问题,所以易选用向量量,所以建立如图所示坐标系,先求得相关点的坐标,进而求得相关向量的坐标,最后用向量夹角公式求解。
建立如图所示坐标系,令正四棱锥的棱长为2,则A(1,-1,0),D(-1,-1,0),

 ,可知
,可知 ,故选C.
,故选C.点评:解决该试题的关键是能建立坐标系,运用向量法表示向量的夹角得到结论,属于基础题。

练习册系列答案
相关题目
 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, .
.

 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. 、
、 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )




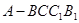 中,
中, 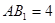 ,底面ABC是正三角形,
,底面ABC是正三角形,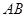 =2.四边形
=2.四边形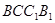 是矩形,二面角
是矩形,二面角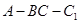 为直二面角,D为
为直二面角,D为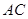 中点。
中点。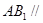 平面
平面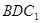 ;
;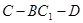 的余弦值.
的余弦值. 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点 ,使得
,使得 的概率是( )
的概率是( )



 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
,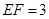 ,
, ,
,  是
是 的中点.
的中点.
 平面
平面 ;
; ;
;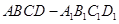 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.
 中,E为AC中点
中,E为AC中点

 ,
,